Primos de Mersenne

Lembramos que um número de Mersenne é um número da forma M_p = 2^p - 1. Vejamos primeiramente que 2^p - 1 só tem chance de ser primo quando p é primo.

Proposição 3.11: Se 2ⁿ - 1 é primo então n é primo.

Dem: Se n = ab com $a, b \ge 2$ então 1 < 2^a - 1 < 2ⁿ - 1 e $2^n - 1 = 2^{ab} - 1 = (2^a)^b - 1 \equiv 1^b - 1 = 0 \pmod {2^a - 1}$e 2ⁿ - 1 é composto.          $\blacksquare$

Por outro lado, não se sabe demonstrar nem que existam infinitos primos de Mersenne nem que existem infinitos primos ppara os quais M_p é composto. Conjectura-se, entretanto, que existam infinitos primos ppara os quais M_p é primo e que, se p_n é o n-ésimo primo deste tipo, temos

$$0 < A < \frac{\log p_n}{n} < B < +\infty$$

para constantes A e B. Existem algumas conjecturas mais precisas quanto ao valor de

$$\lim_{n \to \infty} \sqrt[n]{p_n};$$

Eberhart conjectura que este limite exista e seja igual a 3/2; Wagstaff por outro lado conjectura que o limite seja

$$2^{e^{-\gamma}} \approx 1,4757613971$$

onde $\gamma$ é a já mencionada constante de Euler-Mascheroni.

Primos de Mersenne são interessantes também por causa de números perfeitos. Dado $n \in {\mathbb{N} }^\ast$, definimos

$$\sigma(n) = \sum_{d\vert n} d,$$

a soma dos divisores (positivos) de n. Pelo teorema fundamental da aritmética demonstramos facilmente que se

$$n = p_1^{e_1} p_2^{e_2} \cdots p_m^{e_m},$$

com $p_1 < p_2 < \cdots < p_m$ então
$$\begin{align}\sigma(n) &= (1 + p_1 + \cdots + p_1^{e_1})\cdots (1 + p_m + \cdots... ... + 1} - 1}{p_1 - 1} \cdots \frac{p_m^{e_m + 1} - 1}{p_m - 1}. \notag \end{align}$$
Em particular, se (a,b) = 1 então $\sigma(ab) = \sigma(a) \sigma(b)$. Um inteiro positivo n é dito perfeito se $\sigma(n) = 2n$; os primeiros números perfeitos são 6, 28 e 496. Nosso próximo resultado caracteriza os números perfeitos pares.

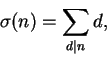
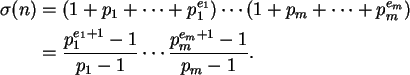
Proposição 3.12: Se M_p é um primo de Mersenne então 2^p-1 M_p é perfeito. Além disso, todo número perfeito par é da 2^p-1 M_p para algum primo p, sendo M_p um primo de Mersenne.

Dem: Se M_p é primo então

$$\sigma(2^{p-1} M_p) = (2^p - 1)(M_p + 1) = 2 \cdot 2^{p-1} M_p.$$

Por outro lado seja n = 2^k b, com k > 0 e b ímpar, um número perfeito par. Temos $\sigma(n) = 2n = \sigma(2^k) \sigma(b)$ donde $2^{k+1} b = (2^{k+1} - 1) \sigma(b) \ge (2^{k+1} - 1)(b+1)$, valendo a igualdade apenas se b for primo. Desta desigualdade temos $b \le 2^{k+1} - 1$. Por outro lado, como (2^k+1 - 1)| 2^k+1 b e (2^k+1 - 1, 2^k+1) = 1, temos (2^k+1 - 1)|be $2^{k+1} - 1 \le b$. Assim b = 2^k+1 - 1 e 2^k+1 b = (2^k+1 - 1)(b+1), donde b é primo. Pela proposição 3.9, p = k+1 é primo, b = M_p e n = 2^p-1 M_p.          $\blacksquare$

Por outro lado, um dos problemas em aberto mais antigos da matemática é o da existência de números perfeitos ímpares. Sabe-se apenas que um número perfeito ímpar, se existir, deve ser muito grande (mais de 300 algarismos) e satisfazer simultaneamente várias condições complicadas.

Conjectura 3.13: Não existe nenhum número perfeito ímpar.

Nosso próximo resultado é o critério de Lucas-Lehmer, a base dos algoritmos que testam para grandes valores de pse 2^p - 1 é ou não primo:

Teorema 3.14: Seja S a seqüência definida por S₀ = 4, S_k+1 = S_k² - 2 para todo natural k. Seja n > 2; M_n = 2ⁿ - 1 é primo se e somente se S_n-2 é múltiplo de M_n.

Dem: Observemos inicialmente que

$$S_n = (2+\sqrt{3})^{2^n} + (2-\sqrt{3})^{2^n}$$

para todo natural n. A demonstração por indução é simples: claramente $S_0 = 4 = (2+\sqrt{3})^{2^0} + (2-\sqrt{3})^{2^0}$ e
$$\begin{align}S_{k+1} &= S_k^2 - 2 \notag\\ &= ((2+\sqrt{3})^{2^k} + (2-\sqrt{3}... ... \notag\\ &= (2+\sqrt{3})^{2^{k+1}} + (2-\sqrt{3})^{2^{k+1}}.\notag \end{align}$$

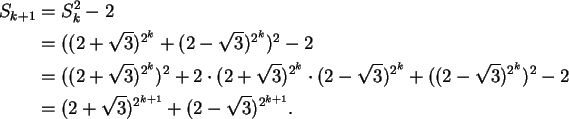
Suponha por absurdo que $M_n \vert (2+\sqrt{3})^{2^{n-2}} + (2-\sqrt{3})^{2^{n-2}}$e que M_n seja composto, com um fator primo q com q² < M_n. Teremos $(2+\sqrt{3})^{2^{n-2}} + (2-\sqrt{3})^{2^{n-2}} \equiv 0 \pmod q$donde, no grupo multiplicativo $G = ({\mathbb{Z} }/(q) [\sqrt{3}])^\ast$, temos $(2+\sqrt{3})^{2^{n-2}} = - (2-\sqrt{3})^{2^{n-2}}.$Como $2 - \sqrt{3} = (2 + \sqrt{3})^{-1}$ esta equação pode ser reescrita como $(2+\sqrt{3})^{2^{n-1}} = -1$ (ainda em G), o que significa que a ordem de $2+\sqrt{3}$ em G é exatamente 2ⁿ. Isto é um absurdo, pois o número de elementos de G é apenas q² - 1 < 2ⁿ. Fica portanto demonstrado que se S_n-2 é múltiplo de M_nentão M_n é primo.

Suponha agora M_n primo, n > 2. Lembramos que n é um primo ímpar. Por reciprocidade quadrática temos $(\frac{3}{M_n}) = - (\frac{M_n}{3}) = -1$, pois $3 \equiv M_n \equiv -1 \pmod 4$ e $M_n \equiv 1 \pmod 3$. Assim, 3 não é um quadrado em ${\mathbb{Z} }/(M_p)$ e $K = {\mathbb{Z} }/(M_p)[\sqrt{3}]$ é um corpo de ordem M_n². Queremos provar que $(2+\sqrt{3})^{2^{n-2}} + (2-\sqrt{3})^{2^{n-2}} \equiv 0 \pmod M_p$, ou seja, que é igual a 0 em K. Isto equivale a demonstrarmos que temos $(2+\sqrt{3})^{2^{n-2}} = - (2-\sqrt{3})^{2^{n-2}}$ em K, o que pode ser reescrito como $(2+\sqrt{3})^{2^{n-1}} = -1$; devemos portanto provar que a ordem de $2+\sqrt{3}$ é exatamente 2ⁿ. Note que 2ⁿ = M_n + 1 donde $(2 + \sqrt{3})^{2^n} = (2 + \sqrt{3})^{M_n} (2 + \sqrt{3}) = (2 - \sqrt{3}) (2 + \sqrt{3}) = 1$; assim é claro que a ordem de $2+\sqrt{3}$ é um divisor de 2ⁿ.

Como $K^\ast$ tem M_n² - 1 = 2ⁿ⁺¹(2^n-1 - 1) elementos, devemos provar que $2+\sqrt{3}$ não é uma quarta potência em K. Note que $(2 + \sqrt{3})^{2^n} = 1$ demonstra que $2+\sqrt{3}$é um quadrado, o que aliás pode ser visto mais diretamente: $2 + \sqrt{3} = (1 + \sqrt{3})^2/2$e 2 = 2ⁿ⁺¹ = 2⁽ⁿ⁺¹⁾² é uma quarta potência em K. Resta-nos assim demonstrar que $\pm(1 + \sqrt{3})$ não são quadrados em K. Suponha por absurdo que $\epsilon (1 + \sqrt{3}) = (a + b \sqrt{3})^2$, com $\epsilon = \pm 1$; temos $\epsilon (1 - \sqrt{3}) = (a - b \sqrt{3})^2$e, multiplicando, -2 = (a² - 3 b²)², o que significa que -2 é um quadrado módulo M_n(pois a e b são inteiros). Isto, entretanto, é claramente falso: $(\frac{-2}{M_n}) = (\frac{-1}{M_n}) (\frac{2}{M_n}) = -1 \cdot 1 = -1$, pois $M_n \equiv 3 \pmod 4$ e já vimos que 2 é um quadrado módulo M_p. Isto conclui a demonstração.          $\blacksquare$

Mesmo quando M_p não é primo, podemos garantir que seus fatores primos serão de certas formas especiais. Isto é muito útil quando procuramos primos de Mersenne pois podemos eliminar alguns expoentes encontrando fatores primos de M_p. Isto também pode ser útil para conjecturarmos quanto à ``probabilidade'' de M_p ser primo, ou, mais precisamente, quanto à distribuição dos primos de Mersenne.

Proposição 3.15: Sejam p > 2 e q primos com q um divisor de M_p. Então $q \equiv 1 \pmod p$ e $q \equiv \pm 1 \pmod 8$.

Dem: Se q divide M_p então $2^p \equiv 1 \pmod q$, o que significa que a ordem de 2 módulo q é p (pois p é primo). Isto significa que p é um divisor de q - 1, ou seja, que $q \equiv 1 \pmod p$. Por outro lado, $2 \equiv 2^{p+1} = (2^{(p+1)/2})^2 \pmod q$, donde $(\frac{2}{q}) = 1$, o que significa que $q \equiv \pm 1 \pmod 8$.          $\blacksquare$

Os vários valores de p para os quais a primalidade de M_p foi testada sugerem que para a ampla maioria dos valores de p, M_p não é primo. Isto é apenas uma conjectura: não se sabe demonstrar sequer que existem infinitos primos ppara os quais M_p seja composto. Vamos agora ver uma proposição que serve para garantir que para certos valores especiais de p, alguns muito grandes, M_p não é primo.

Proposição 3.16: Seja p primo, $p\equiv 3 \pmod 4$. Então 2p + 1 é primo se e somente se 2p + 1 divide M_p.

Dem: Se q é primo então $M_p = 2^p - 1 = 2^{(q-1)/2} - 1 \equiv (\frac{2}{q}) - 1 \pmod q$. Mas $p\equiv 3 \pmod 4$ significa que $q \equiv 7 \pmod 8$, donde $(\frac{2}{q}) = 1$. Assim, $M_p \equiv 0 \pmod q$, o que demonstra uma das implicações da proposição.

Por outro lado, se 2p + 1 não é primo tem fatores primos r com $r \not\equiv 1 \pmod p$ (pois r < p). Se 2p + 1 dividisse M_p, r seria um fator primo de M_p, contrariando a proposição anterior.          $\blacksquare$

Os primos p para os quais 2p+1 é primo são chamados de primos de Sophie Germain. Alguns primos de Sophie Germain bastante grandes são conhecidos, como $p_0 = 18458709 \cdot 2^{32611} - 1$; assim, pela proposição anterior, M_p0 é composto. Sabe-se também que se $\pi_{\text{SG}}(x)$ denota o número de primos de Sophie Germain menores do que x então existe C tal que para todo x

$$\pi_{\text{SG}}(x) < C \frac{x}{(\log x)^2}.$$

Acredita-se que $\pi_{\text{SG}}(x)$ seja assintótico a $cx/(\log x)^2$para algum c > 0 mas não se sabe demonstrar sequer que existem infinitos primos de Sophie Germain.