Outros resultados e conjecturas sobre primos

Nesta seção veremos o enunciado de alguns resultados clássicos sobre números primos. Também veremos vários problemas em aberto famosos.

Teorema 1.29: (Dirichlet) Dados naturais a, d com $\operatorname{mdc}(a,d) = 1$, existem infinitos primos da forma a + dn (com n natural).

A demonstração usual deste teorema usa variáveis complexas. Muitos casos particulares admitem demonstrações elementares mais ou menos simples. O leitor não deve ter dificuldade em demonstrar, por exemplo, que existem infinitos primos da forma 4n + 3 ou 6n + 5.

Existem vários refinamentos conhecidos do teorema de Dirichlet. Definimos $\pi_{d,a}(x)$ como sendo o número de primos da forma a + dn no intervalo [2,x]. De la Vallée Poussin provou que

$$lim_{x \to +\infty} \frac{\pi_{d,a}(x)}{\pi(x)} = \frac{1}{\varphi(d)},$$

isto é, todas as possíveis classes módulo d têm aproximadamente a mesma proporção de primos.

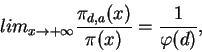
Por outro lado, Tchebycheff observou que para valores pequenos de x, $\pi_{3,2}(x) - \pi_{3,1}(x)$ e $\pi_{4,3}(x) - \pi_{4,1}(x)$são positivos. Um teorema de Littlewood, entretanto, demonstra que estas funções mudam de sinal infinitas vezes. Em 1957, Leech demonstrou que o menor valor de x para o qual $\pi_{4,3}(x) - \pi_{4,1}(x) = -1$ é 26861 e em 1978 Bays e Hudson demonstraram que o menor valor de x para o qual $\pi_{3,2}(x) - \pi_{3,1}(x) = -1$ é 608981813029.

Seja p(d,a) o menor primo da forma a + dn, n inteiro e

$$p(d) = \max \{ p(d,a) \mid 0 < a < d, \operatorname{mdc}(a,d) = 1\}.$$

Linnik (1944) provou que existe L > 1 com p(d) < d^Lpara todo d suficientemente grande. A melhor estimativa conhecida para L é $L \le 5,5$, devida a Heath-Brown (1992), que também conjecturou que

$$p(d) \le C d (\log d)^2.$$

Por outro lado, não se sabe demonstrar que existam infinitos primos da forma n² + 1; aliás, não existe nenhum polinômio P em uma variável e de grau maior que 1 para o qual se saiba demonstrar que existem infinitos primos da forma P(n), $n \in {\mathbb{Z} }$. Por outro lado, existem muitos polinômios em mais de uma variável que assumem infinitos valores primos: por exemplo, prova-se facilmente que todo primo da forma 4n + 1pode ser escrito também na forma a² + b², $a, b \in {\mathbb{Z} }$. Por outro lado, Friedlander e Iwaniec provaram recentemente um resultado muito mais difícil: que existem infinitos primos da forma a² + b⁴.

Um dos problemas em aberto mais famosos da matemática é a conjectura de Goldbach: todo número par maior ou igual a 4 é a soma de dois primos. Chen demonstrou que todo número par suficientemente grande é a soma de um primo com um número com no máximo dois fatores primos. Vinogradov demonstrou que todo ímpar suficientemente grande (por exemplo, maior do que 3³¹⁵) é uma soma de três primos.

Quando p e p+2 são ambos primos, dizemos que eles são primos gêmeos. Conjectura-se, mas não se sabe demonstrar, que existem infinitos primos gêmeos. Brun, por outro lado, provou que primos gêmeos são escassos no seguinte sentido: se $\pi_2(x)$ é o número de pares de primos gêmeos até x então

$$\pi_2(x) < \frac{100 x}{(\log x)^2}$$

para x sufientemente grande. Em particular,

$$\sum_{p \text{ primo gêmeo}} \frac{1}{p} < +\infty.$$

Acredita-se que $\pi_2(x)$ seja assintótico a $Cx/(\log x)^2$para alguma constante positiva C. Deixamos como exercício provar a seguinte caracterização de primos gêmeos devida a Clement. Seja $n \ge 2$; os inteiros n e n+2 são ambos primos se e somente se

$$4((n-1)! + 1) + n \equiv 0 \pmod {n(n+2)}.$$

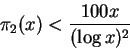
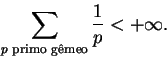
Seja p_n o n-ésimo número primo. O teorema dos números primos equivale a dizer que

$$\lim_{n \to \infty} \frac{p_n}{n \log n} = 1.$$

Por outro lado, sabe-se muito pouco sobre o comportamento da função d_n = p_n+1 - p_n. Por exemplo, a conjectura de que existem infinitos primos gêmeos equivale a dizer que $\liminf d_n = 2$. Não se sabe provar nem que

$$L = \liminf \frac{d_n}{\log p_n} = 0;$$

Erdös provou que L < 1 e Maier que $L \le 0,248$. Erdös também provou que o conjunto D dos pontos de acumulação de $d_n/\log p_n$ tem medida positiva, resultado que foi posteriormente melhorado por Hildebrand e Maier ([HM]), que provaram entre outras coisas que existe uma constante positiva ctal que se x é suficientemente grande, a medida de Lebesgue de $D \cap [0,x]$ é maior ou igual a cx. Por outro lado, é um teorema clássico, conhecido como postulado de Bertrand, que sempre existe pelo menos um primo entre m e 2m, ou seja, d_n < p_n. Em 1931, Westzynthius provou que

$$\limsup \frac{d_n}{\log p_n} = \infty,$$

e em 1963 Rankin, completando um trabalho de Erdös, mostrou que

$$\limsup \frac{d_n (\log\log\log p_n)^2 }% {\log p_n \log\log p_n \log\log\log\log p_n} \ge e^\gamma \approx 1,78107$$

onde $\gamma$ é a constante de Euler-Mascheroni,

$$\gamma = \lim_{n \to \infty} \left({1 + \frac{1}{2} + \cdots + \frac{1}{n} - \log n }\right) \approx 0,5772156649;$$

este resultado foi melhorado posteriormente por Pomerance e Pintz, que provou que o lado esquerdo é maior ou igual a $2 e^\gamma$ ([Pintz]). Conjectura-se que

$$\limsup \frac{d_n}{(\log p_n)^2} = C$$

para alguma constante positiva C. Outra conjectura famosa é que sempre há pelo menos um primo entre n² e (n+1)². Observamos que a primeira vez que d_n > 1000 ocorre para p_n = 1693182318746371, quando d_n = 1132, o que foi descoberto recentemente por T. Nicely e D. Nyman.

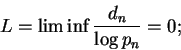
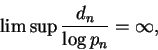
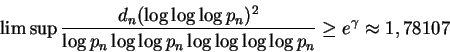
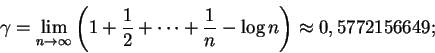
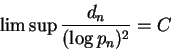
Sierpinski provou que existem infinitos números naturais ktais que $k \cdot 2^n + 1$ é composto para todo natural ne Riesel provou o mesmo resultado para $k \cdot 2^n - 1$. Conjectura-se que os menores valores de k com as propriedades acima são respectivamente 78557 e 509203. Há um projeto cooperativo, que consiste em procurar primos grandes, para demonstrar estas conjecturas (veja http://vamri.xray.ufl.edu/proths/).

Outro problema famoso é o de determinar se existem progressões aritméticas arbitrariamente longas formadas exclusivamente por primos. Van der Corput provou em 1939 que há uma infinidade de progressões aritméticas formadas por 3 primos ([Corput]). Uma resposta afirmativa ao problema geral seguiria da veracidade de uma conjectura de Erdös, segundo a qual se $A \subseteq {\mathbb{N} }$é tal que a série dos inversos de seus elementos diverge, então A contém progressões aritméticas arbitrariamente longas. Atualmente, a maior progressão aritmética de primos que se conhece é formada pelos 22 termos 11410337850553+4609098694200k, com $0\le k\le 21$, e foi encontrada por Pritchard et al. em 1993.

M. Toplic, um dos membros de um projeto conjunto realizado com o auxílio da internet, encontrou em 15/01/1998 o primeiro exemplo de 10 números primos consecutivos em progressão aritmética, que são os primos p+210k com $0\le k\le 9$, onde
$$\begin{align}p = &10099697246971424763778665558796984032950932468 \notag\\ &9190041803603417758904341703348882159067229719. \notag \end{align}$$

Por outro lado, em 23/4/1999, um grupo de 6 pesquisadores achou 10 primos palíndromos (i.e., cuja representação decimal é simétrica) consecutivos (dentre os primos palíndromos) em progressão aritmética, que são

$$p+1010100000000000k, \quad\text{ com }\quad 0\le k\le 9,$$

onde

p=742950290870000078092059247.

O leitor interessado em aprender mais sobre problemas em aberto em teoria dos números pode consultar [Guy].