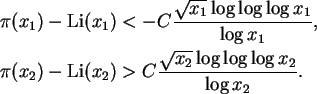Já vimos que existem infinitos primos;
o teorema dos números primos dá uma estimativa de quantos primos
existem até um inteiro x, ou seja, descreve a distribuição dos primos.
Defina ![]() como sendo o número de primos p com
como sendo o número de primos p com
![]() .
.
Teorema 1.26: (Teorema dos números primos)
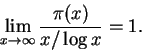
Observe que aqui e em todo o livro ![]() denota o logaritmo natural.
Este resultado foi conjecturado por vários matemáticos,
inclusive por Legendre e Gauss, mas a demonstração completa só foi
encontrada em 1896, por de la Vallée Poussin e Hadamard (independentemante).
Não demonstraremos este teorema:
as demonstrações elementares conhecidas são todas bastante difíceis
(lembramos que uma demonstração é dita elementar
quando não usa ferramentas avançadas:
muitas demonstrações elementares são longas e sofisticadas).
Daremos uma demonstração da seguinte proposição (devida a Tchebycheff)
que é claramente uma versão fraca do teorema dos números primos.
denota o logaritmo natural.
Este resultado foi conjecturado por vários matemáticos,
inclusive por Legendre e Gauss, mas a demonstração completa só foi
encontrada em 1896, por de la Vallée Poussin e Hadamard (independentemante).
Não demonstraremos este teorema:
as demonstrações elementares conhecidas são todas bastante difíceis
(lembramos que uma demonstração é dita elementar
quando não usa ferramentas avançadas:
muitas demonstrações elementares são longas e sofisticadas).
Daremos uma demonstração da seguinte proposição (devida a Tchebycheff)
que é claramente uma versão fraca do teorema dos números primos.
Proposição 1.27:
Existem constantes positivas c < C tais que
Dem:
Observemos inicialmente que
![]() é
múltiplo de todos os primos p que satisfazem
é
múltiplo de todos os primos p que satisfazem
![]() .
Como
.
Como
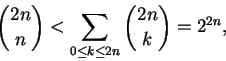
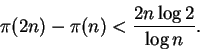
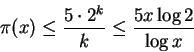
Vamos agora provar a outra desigualdade.
O expoente do primo p na fatoração de n! é
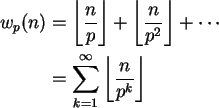
(esta é uma soma finita pois se
![]() então
então
![]() ).
De fato,
).
De fato,
![]() é sempre 0 ou 1,
e é igual a 1 se e só se pj divide n+1.
Assim,
wp(n+1) - wp(n)é igual ao expoente de p na fatoração de n+1,
o que fornece uma prova por indução do fato acima.
é sempre 0 ou 1,
e é igual a 1 se e só se pj divide n+1.
Assim,
wp(n+1) - wp(n)é igual ao expoente de p na fatoração de n+1,
o que fornece uma prova por indução do fato acima.
Assim, o expoente de p em
![]() é
é
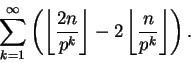
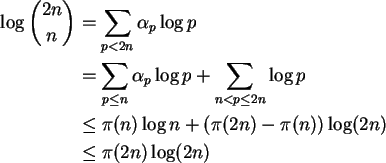
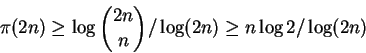
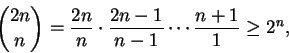
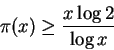
Corolário 1.28:
Seja
![]() uma função decrescente.
A série
uma função decrescente.
A série

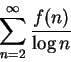
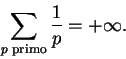
Deixamos a demonstração deste corolário como exercício.
Uma aproximação mais precisa para ![]() é dada por
é dada por
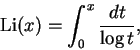
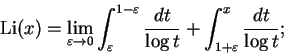
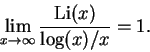
A hipótese de Riemann, já mencionada, equivale a dizer que
para todo
![]() existe C com
existe C com