A lei de Gauss de reciprocidade quadrática afirma que se p e q são primos há uma relação direta entre p ser quadrado módulo qe q ser quadrado módulo p. Este teorema fornece um rápido algoritmo para determinar se a é quadrado módulo p onde a é um inteiro e p um número primo.
Definição 2.16:
Seja p um primo e a um inteiro. Definimos o
símbolo de Lagrange
![]() por
por

Proposição 2.17:
Seja p um primo ímpar e
![]() tal que
tal que
![]() . Então
. Então
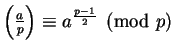 .
.
Dem:
Sabemos que se ![]() então
então
![]() ,
ou seja, Xp-1-1 tem como raízes
,
ou seja, Xp-1-1 tem como raízes
![]() em
em
![]() .
Por outro lado,
.
Por outro lado,
![]() .
Se existe
.
Se existe
![]() tal que
tal que
![]() então
então
![]() ;
ou seja,
;
ou seja,
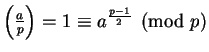 .
Como
.
Como
![]() ,
há pelo menos
,
há pelo menos
![]() quadrados em
quadrados em
![]() ,
logo os quadrados
são exatamente as raízes de
,
logo os quadrados
são exatamente as raízes de
![]() em
em
![]() ,
donde os não
quadrados são exatamente as raízes de
,
donde os não
quadrados são exatamente as raízes de
![]() ,
ou seja, se
,
ou seja, se
![]() então
então
![]() .
.
![]()
Corolário 2.18:
Se p é primo ímpar então
![]() .
.
Vamos agora reinterpretar a Proposição 1.
Seja
![]() .
Para cada
.
Para cada
![]() escrevemos
escrevemos ![]() como
como
![]() com
com
![]() e
e
![]() .
Se
.
Se
![]() temos
temos
![]() ou
ou
![]() ;
a primeira possibilidade implica i = j e a segunda é impossível.
Assim, se
;
a primeira possibilidade implica i = j e a segunda é impossível.
Assim, se ![]() temos
temos
![]() donde
donde
![]() .
Assim
.
Assim
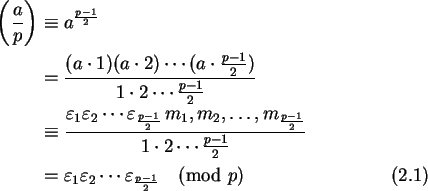
donde
![]() ,
pois ambos pertencem a
,
pois ambos pertencem a ![]() .
Assim,
.
Assim,
![]() onde m é o número de
elementos j de
onde m é o número de
elementos j de
![]() tais que
tais que
![]() .
Como primeira conseqüência deste fato temos o seguinte resultado.
.
Como primeira conseqüência deste fato temos o seguinte resultado.
Proposição 2.19:
Se p é um primo ímpar então
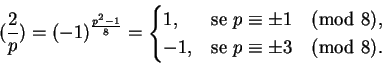
Dem:
Se
![]() ,
digamos p=4k+1, temos
,
digamos p=4k+1, temos
![]() .
Como
.
Como
![]() para
para ![]() e
e
![]() para
para
![]() ,
temos
,
temos
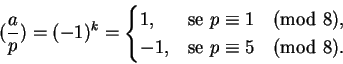
Se
![]() ,
digamos p = 4k+3, temos
,
digamos p = 4k+3, temos
![]() .
Para
.
Para
![]() temos
temos
![]() e
para
e
para
![]() temos
temos
![]() ,
donde
,
donde
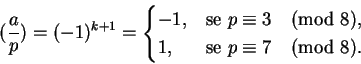
Teorema 2.20: (Lei de reciprocidade quadrática)
Sejam p e q primos ímpares. Então
![]() .
.
Dem:
Na notação acima, com a=q, para cada ![]() ,
onde
,
onde