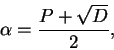
Suponha dados inteiros n > 1, P e Qtais que
D = P2 - 4Q não é um quadrado módulo n.
Seja
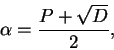
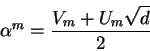
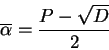
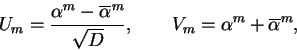
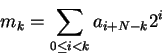
Lembramos que vimos no capítulo anterior que se p > 2é primo e d não é um quadrado módulo p então
![]() é um corpo com p2 elementos.
é um corpo com p2 elementos.
Proposição 3.17:
Se n é primo e D não é um quadrado módulo nentão
![]() em
em
![]() .
.
Dem:
Suponhamos que n seja primo.
Em K temos a identidade
(X+Y)n = Xn + Yn:
ela segue do binômio de Newton e do fato que
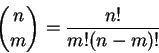
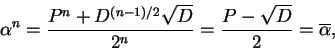
Analogamente, se n é primo, temos
![]() em K.
Assim, ainda em K,
em K.
Assim, ainda em K,
![]() .
Segue da fórmula para Um que
.
Segue da fórmula para Um que
![]() .
Proclamamos este resultado como uma proposição:
.
Proclamamos este resultado como uma proposição:
Proposição 3.18:
Se n é primo ímpar,
![]() e as seqüências Um e Vm são definidas pelas recorrências
e as seqüências Um e Vm são definidas pelas recorrências
![]()
então
![]() .
.
Dem: Acima.
![]()
Esta proposição nos dá mais um algoritmo para testar a primalidade de n.
Proposição 3.19:
Se ![]() é primo,
é primo, ![]() ,
,
![]() e D é quadrado módulo nentão
e D é quadrado módulo nentão
![]() .
.
Dem:
No anel
![]() ,
2 é invertível, assim como D e
,
2 é invertível, assim como D e ![]() .
Em K temos, portanto,
.
Em K temos, portanto,
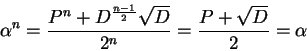
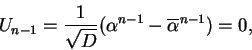
Em suma, se ![]() é primo,
é primo, ![]() ,
,
![]() então
então
![]() é múltiplo de n,
o que se deve ao fato de
é múltiplo de n,
o que se deve ao fato de ![]() ser igual a
ser igual a
![]() se
se
![]() no anel
no anel
![]() .
Observemos agora que se
.
Observemos agora que se
![]() em Kentão existe um inteiro r tal que
em Kentão existe um inteiro r tal que
Proposição 3.20:
Se ![]() é primo,
é primo, ![]() e
e ![]() então,
para todo natural
então,
para todo natural ![]() ,
,
![]() é
múltiplo de nk, onde
é
múltiplo de nk, onde
![]() .
.
Dem:
Vamos supor, por hipótese de indução, que
![]() ,
,
![]() .
Elevando os dois lados da equação à n-ésima potência
temos
.
Elevando os dois lados da equação à n-ésima potência
temos
Proposição 3.21:
Sejam ![]() com
com
![]() , e (Uk)uma seqüência de Lucas
(com U0 = 0, U1=1 e
Uk+2 = PUk+1 - QUk).
Se
, e (Uk)uma seqüência de Lucas
(com U0 = 0, U1=1 e
Uk+2 = PUk+1 - QUk).
Se
![]() é não vazio então existe
é não vazio então existe
![]() tal que
tal que
![]() se e somente se
se e somente se ![]() .
Tal a será denotado por
.
Tal a será denotado por
![]() .
.
Dem:
Observemos inicialmente que para todo
![]() ,
,
![]() temos
Um+n = UmUn+1 - QUm-1Un . De fato, considerando mfixo e n variável, os dois lados da igualdade satisfazem a mesma recorrência
de segunda ordem
Xk+2 = PXk+1 - QXk ,
temos
Um+n = UmUn+1 - QUm-1Un . De fato, considerando mfixo e n variável, os dois lados da igualdade satisfazem a mesma recorrência
de segunda ordem
Xk+2 = PXk+1 - QXk ,
![]() ,
e
temos, para n=0,
,
e
temos, para n=0,
![]() (pois
U1=1 e U0=0), e, para m=1,
(pois
U1=1 e U0=0), e, para m=1,
![]() (pois U2=P, U1=1 e
Um+1 = PUm - QUn-1), o que implica a
igualdade para todo
(pois U2=P, U1=1 e
Um+1 = PUm - QUn-1), o que implica a
igualdade para todo
![]() .
.
Como conseqüência, se
![]() e
e ![]() então
então
![]() . Por
outro lado, se
. Por
outro lado, se
![]() e
e ![]() , com
, com ![]() então, como
(fazendo
então, como
(fazendo ![]() ,
,
![]() )
)
![]() temos que r divide
temos que r divide
![]() , mas
, mas
![]() e
e
![]() divide
divide
![]() (o que pode ser
facilmente provado por indução a partir de
(o que pode ser
facilmente provado por indução a partir de
![]() ), donde
), donde
![]() também é igual a 1, logo
também é igual a 1, logo
![]() . Assim,
. Assim,
![]() , e
, e
![]() ,
,
![]() , o que implica que Ar é
da forma descrita, com
, o que implica que Ar é
da forma descrita, com
![]() (de fato, se existe
(de fato, se existe ![]() que não
seja múltiplo de a, existiriam b e c naturais com k = ab+c, 0 <
c < a, mas
que não
seja múltiplo de a, existiriam b e c naturais com k = ab+c, 0 <
c < a, mas ![]() e, como
e, como ![]() ,
,
![]() , logo
c=k-ab pertenceria a Ar , contradizendo a definição de a.
, logo
c=k-ab pertenceria a Ar , contradizendo a definição de a.
![]()
Teorema 3.22:
Seja n > 1 um inteiro ímpar. Se existe um inteiro
d primo com n tal que para todo fator primo r de n+1existem P(r), Q(r) e m(r) inteiros com
![]() e
e
![]() tais que a seqüência
de Lucas associada
(Uk(r)) satisfaz
tais que a seqüência
de Lucas associada
(Uk(r)) satisfaz
![]() e
e
![]() então n é primo.
então n é primo.
Dem:
Seja
![]() a
fatoração prima de n+1.
As hipóteses implicam que
a
fatoração prima de n+1.
As hipóteses implicam que
![]() divide
divide
![]() para
para
![]() .
Por outro lado, se
.
Por outro lado, se
![]() é a fatoração prima de n,
segue da Proposição 3.20 que
é a fatoração prima de n,
segue da Proposição 3.20 que
![]() divide
divide
![]() (A hipótese
(A hipótese
![]() é satisfeita.
De fato, como
é satisfeita.
De fato, como
![]() ,
,
![]() não divide D(ri), e,
se
não divide D(ri), e,
se ![]() dividisse Q(ri),
dividisse Q(ri), ![]() não dividiria P(ri),
e teríamos
não dividiria P(ri),
e teríamos
![]() para todo
para todo ![]() ,
e
,
e ![]() não dividiria
Uk(ri) para nenhum
não dividiria
Uk(ri) para nenhum ![]() ,
contradizendo o fato de n dividir
Un+1(ri)).
Assim, se
,
contradizendo o fato de n dividir
Un+1(ri)).
Assim, se
![]() ,
,
![]() temos que
temos que
![]() divide
UM(ri),
para
divide
UM(ri),
para
![]() ,
,
![]() .
Isso implica que
.
Isso implica que
![]() divide
UM(ri) para
divide
UM(ri) para
![]() ,
e portanto
,
e portanto
![]() para
para
![]() ,
donde n+1 divide M.
Temos agora duas possibilidades:
,
donde n+1 divide M.
Temos agora duas possibilidades:
(i) s=1. Nesse caso temos que n+1 divide
![]() o que é absurdo
se
o que é absurdo
se
![]() ,
pois teríamos
,
pois teríamos
![]() ,
e se
,
e se
![]() temos que
temos que
![]() divide
divide
![]() ,
o que implica
,
o que implica ![]() ,
ou seja, n é primo.
,
ou seja, n é primo.
(ii) ![]() . Nesse caso
. Nesse caso
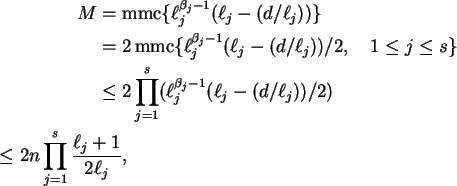
que é sempre menor que n(pois
![]() )
e portanto é um absurdo que n+1 divida M.
)
e portanto é um absurdo que n+1 divida M.
![]()
A seguinte proposição, devida a Morrison, é análoga ao resultado de Pocklington:
Proposição 3.23:
Seja N > 1 um inteiro ímpar e N+1=FR.
Se existe um inteiro d primo com N tal que para todo fator primo r de Fexiste uma seqüência de Lucas Un(r) associada a inteiros
P(r), Q(r) e um inteiro m(r) primo com Ne
![]() tal que
tal que
![]() e
e
![]() então cada fator primo
então cada fator primo ![]() de
N satisfaz
de
N satisfaz
![]() .
.
Dem:
Se
![]() é a
fatoração prima de F então
é a
fatoração prima de F então
![]() para
para
![]() .
Se
.
Se ![]() é um fator primo de N,
também temos
é um fator primo de N,
também temos
![]() .
Como
.
Como
![]() segue que
segue que
![]() , donde
, donde
![]() , e portanto
, e portanto
![]() divide
divide
![]() para
para
![]() .
Por outro lado,
.
Por outro lado,
![]() divide
divide
![]() ,
donde
,
donde
![]() divide
divide
![]() para
para
![]() divide
divide
![]() .
.
![]()
Corolário 3.24: Nas condições da proposição, se F > R então N é primo.
Dem:
Qualquer fator primo de N deve ser congruente a 1 ou a
-1 módulo F, mas, se N é composto, deve ter um fator primo menor ou igual
à sua raiz quadrada, que deve, pois, ser igual a F-1. Como
![]() ,
F2-1 > N, logo
,
F2-1 > N, logo
![]() ,
donde o outro fator
primo de N também deve ser igual a F-1, e teríamos
,
donde o outro fator
primo de N também deve ser igual a F-1, e teríamos
![]() ,
que só seria múltiplo de F se F fosse igual a 2, e F-1igual a 1, absurdo.
,
que só seria múltiplo de F se F fosse igual a 2, e F-1igual a 1, absurdo.
![]()
Proposição 3.25:
Seja n > 1 um inteiro ímpar. Se para todo fator
primo r de n+1 existem
P(r), Q(r) inteiros
com
![]() onde
D(r) = (P(r))2 - 4 Q(r)tais que a seqüência de Lucas associada
(Uk(r)) satisfaz
onde
D(r) = (P(r))2 - 4 Q(r)tais que a seqüência de Lucas associada
(Uk(r)) satisfaz
![]() e
e
![]() então n é primo.
então n é primo.
Dem:
Seja ![]() um fator primo de n.
Para cada fator primo r de n+1temos que
um fator primo de n.
Para cada fator primo r de n+1temos que
![]() e
e
![]() .
Assim, se
.
Assim, se
![]() é a maior potência de rque divide n+1, então
é a maior potência de rque divide n+1, então
![]() divide
divide
![]() ,
como acima.
Em particular,
,
como acima.
Em particular,
![]() divide
divide
![]() ,
donde n+1 divide
,
donde n+1 divide
![]() .
Assim,
.
Assim,
![]() donde
donde
![]() ,
o que implica na primalidade de n pois n não tem nenhum fator
primo menor ou igual à sua raiz quadrada.
,
o que implica na primalidade de n pois n não tem nenhum fator
primo menor ou igual à sua raiz quadrada.
![]()
Vamos agora dar outra prova do critério de Lucas-Lehmer usando os resultados anteriores.
Dem:
A seqüência de Lucas associada a P=2, Q=-2, é dada pela
fórmula
![]() .
Temos
.
Temos
![]() ,
onde
,
onde
![]() .
Além disso,
U2k = UkVk para todo
.
Além disso,
U2k = UkVk para todo
![]() .
.
Para ![]() temos
temos
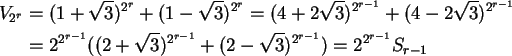
(onde S0=4,
Sm+1 = Sm2-2,
![]() ).
Se n > 2 e
Mn =
2n-1 divide Sn-2 então Mn divide
V2n-1,
logo também divide
UMn+1 = U2n = U2n-1 V2n-1, e, como
).
Se n > 2 e
Mn =
2n-1 divide Sn-2 então Mn divide
V2n-1,
logo também divide
UMn+1 = U2n = U2n-1 V2n-1, e, como
![]() ,
e
Vk2 - 12Uk2 = 4(-2)k, segue
que
V2n-12 - 12U2n-12 = 22n-1+2, e, se Mn dividisse
,
e
Vk2 - 12Uk2 = 4(-2)k, segue
que
V2n-12 - 12U2n-12 = 22n-1+2, e, se Mn dividisse
![]() , dividiria também
22n-1+2, absurdo. Assim,
pelo Teorema 3.22, Mn é primo.
, dividiria também
22n-1+2, absurdo. Assim,
pelo Teorema 3.22, Mn é primo.
Por outro lado, se Mn é primo, como D=12,
![]() ,
logo Mn divide
UMn+1 = U2n, e,
como
,
logo Mn divide
UMn+1 = U2n, e,
como
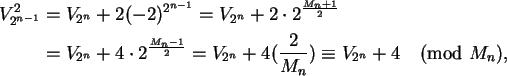
pois
![]() (já sabemos que n deve ser um primo ímpar).
Temos
(já sabemos que n deve ser um primo ímpar).
Temos
![]() ,
que é igual a
,
que é igual a
![]() em
em
![]() (pois
(pois
![]() )
donde
)
donde
![]() e portanto
e portanto
![]() .
Assim, Mn divide Sn-2, o que
conclui nossa nova demonstração do critério de Lucas-Lehmer.
.
Assim, Mn divide Sn-2, o que
conclui nossa nova demonstração do critério de Lucas-Lehmer.
![]()
Se N é um primo ímpar e d não é quadrado módulo
N, então
![]() é um corpo finito com N2 elementos e
portanto existem inteiros a e b tais que
é um corpo finito com N2 elementos e
portanto existem inteiros a e b tais que
![]() é uma raiz primitiva de K.
Sejam
é uma raiz primitiva de K.
Sejam
![]() e, para
e, para
![]() ,
,
![]() .
Temos
U0=0, U1=1 e
Um+2 = 2aUm+1 - (a2-db2)Um para todo
.
Temos
U0=0, U1=1 e
Um+2 = 2aUm+1 - (a2-db2)Um para todo
![]() .
Temos ainda
.
Temos ainda ![]() em K,
senão x pertenceria a
em K,
senão x pertenceria a
![]() e
e
![]() dividiria N-1.
Assim, b e
dividiria N-1.
Assim, b e ![]() são invertíveis em K e,
se P = 2a,
Q = a2 - d b2 então
D = P2 - 4Q = 4d b2satisfaz
são invertíveis em K e,
se P = 2a,
Q = a2 - d b2 então
D = P2 - 4Q = 4d b2satisfaz
![]() .
Pela proposição 3.18,
.
Pela proposição 3.18,
![]() .
Por outro lado, se m é menor que N+1, caso
N divida Um teríamos
.
Por outro lado, se m é menor que N+1, caso
N divida Um teríamos
![]() em K, donde teríamos em K,
em K, donde teríamos em K,
![]() .
Pela proposição 3.17,
.
Pela proposição 3.17,
![]() ,
logo
x(N-1)m = 1, absurdo, pois
,
logo
x(N-1)m = 1, absurdo, pois
![]() .
Isto fornece recíprocas para os resultados desta seção.
.
Isto fornece recíprocas para os resultados desta seção.