



Next: Multiplicação de polinômios usando
Up: Aspectos computacionais
Previous: Alguns programas usando a
A forma de multiplicar inteiros ensinada na escola
é simples e conveniente para inteiros relativamente pequenos,
mas vejamos seu custo.
Para multiplicar dois inteiros de n algarismos na base dprocedemos basicamente a partir da fórmula:
calculamos (ou olhamos na tabuada) todos os produtos de um algarismo
de um dos inteiros com um algarismo do outro,
multiplicamos pela potência de d apropriada
(o que equivale a acrescentar zeros à direita) e somamos as n2parcelas obtidas. Efetuamos no processo n2 multiplicações
e um número comparável de somas;
assim, o tempo gasto com este algoritmo é aproximadamente A n2para alguma constante positiva A.
Se isto fosse o melhor que pudéssemos fazer, o tempo para checar
a primalidade de Mp seria aproximadamente A p3.
Existem entretanto outros algoritmos de multiplicação:
examinemos primeiro um algoritmo relativamente simples,
o algoritmo de Karatsuba,
usado pela biblioteca gmp (e portanto por nossos programas acima).
Sejam A e B dois inteiros com n algarismos cada um.
Se
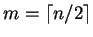 ,
podemos escrever
A = A1 dm + A0,
B = B1 dm + B0 e
AB = A1 B1 d2m + (A1 B0 + A0 B1) dm + A0 B0.
Pelo algoritmo anterior, calcularíamos os quatro produtos
de inteiros com m algarismos.
Entretanto, os produtos A1 B0 e A0 B1não são necessários individualmente,
e podemos calcular sua soma da seguinte forma:
,
podemos escrever
A = A1 dm + A0,
B = B1 dm + B0 e
AB = A1 B1 d2m + (A1 B0 + A0 B1) dm + A0 B0.
Pelo algoritmo anterior, calcularíamos os quatro produtos
de inteiros com m algarismos.
Entretanto, os produtos A1 B0 e A0 B1não são necessários individualmente,
e podemos calcular sua soma da seguinte forma:
A1 B0 + A0 B1 = (A1 - A0)(B0 - B1) + A1 B1 + A0 B0.
Em outras palavras, podemos escrever
AB =
A1 B1 (d2m + dm) + (A1 - A0)(B0 - B1) dm + A0 B0 (dm + 1).
Assim, podemos calcular os três coeficientes
com apenas três multiplicações (ao invés de quatro) e algumas somas.
Mesmo que o número de somas aumente, já sabemos que somas são rápidas
e portanto podemos esperar que este algoritmo represente uma melhora
substancial em relação ao anterior.
Mais precisamente,
repetimos este processo para diminuirmos o tamanho dos inteiros.
Assim, se denotarmos por f(n) o tempo necessário para multiplicar
inteiros de n algarismos temos
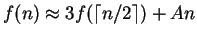 e provamos facilmente que
e provamos facilmente que
onde
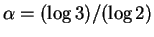 .
.




Next: Multiplicação de polinômios usando
Up: Aspectos computacionais
Previous: Alguns programas usando a
Nicolau C. Saldanha
1999-08-09
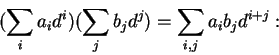
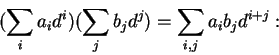
![]() ,
podemos escrever
A = A1 dm + A0,
B = B1 dm + B0 e
AB = A1 B1 d2m + (A1 B0 + A0 B1) dm + A0 B0.
Pelo algoritmo anterior, calcularíamos os quatro produtos
de inteiros com m algarismos.
Entretanto, os produtos A1 B0 e A0 B1não são necessários individualmente,
e podemos calcular sua soma da seguinte forma:
,
podemos escrever
A = A1 dm + A0,
B = B1 dm + B0 e
AB = A1 B1 d2m + (A1 B0 + A0 B1) dm + A0 B0.
Pelo algoritmo anterior, calcularíamos os quatro produtos
de inteiros com m algarismos.
Entretanto, os produtos A1 B0 e A0 B1não são necessários individualmente,
e podemos calcular sua soma da seguinte forma:
![]() e provamos facilmente que
e provamos facilmente que