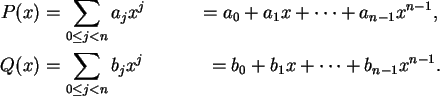
O método aprendido na escola exige n2 multiplicações; o métode de Karatsuba pode ser adaptado para este problema e exige aproximadamente
Suponha que queiramos multiplicar dois polinômios
![]() ,
de grau menor do que n,
representados pelos seus coeficientes:
,
de grau menor do que n,
representados pelos seus coeficientes:
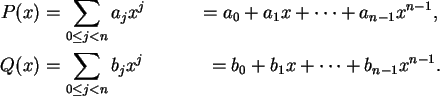
O método aprendido na escola exige n2 multiplicações;
o métode de Karatsuba pode ser adaptado para este problema
e exige aproximadamente ![]() multiplicações,
com
multiplicações,
com
![]() .
Veremos agora como efetuar esta multiplicação com um número
muito menor de operações.
.
Veremos agora como efetuar esta multiplicação com um número
muito menor de operações.
Uma idéia é a de considerar os polinômios como representados
não pelos seus coeficientes e sim pelos seus valores em npontos distintos
![]() .
Temos evidentemente
.
Temos evidentemente
![]() :
se o produto PQ tem grau menor do que n então PQé o único polinômio que assume estes n valores.
A dificuldade em usar este método está em calcular os valores de P e Qnos n pontos
:
se o produto PQ tem grau menor do que n então PQé o único polinômio que assume estes n valores.
A dificuldade em usar este método está em calcular os valores de P e Qnos n pontos
![]() e em recuperar PQ a partir de seu valor nestes mesmos pontos.
Se os valores
e em recuperar PQ a partir de seu valor nestes mesmos pontos.
Se os valores ![]() forem escolhidos sem critério
este método pode acabar sendo mais lento do que os outros que já apresentamos.
Veremos que certas escolhas de n e
forem escolhidos sem critério
este método pode acabar sendo mais lento do que os outros que já apresentamos.
Veremos que certas escolhas de n e ![]() tornam o algoritmo rápido:
uma das mais simples é tomar n uma potência de 2 e
tornam o algoritmo rápido:
uma das mais simples é tomar n uma potência de 2 e
![]() ,
onde
,
onde
![]() é uma raiz da unidade de ordem n.
é uma raiz da unidade de ordem n.
Suponha que
![]() então as potências pares de
então as potências pares de
![]() e
e ![]() coincidem, enquanto as potências ímpares
diferem pelo sinal. Isto nos permite economizar multiplicações
quando calculamos
coincidem, enquanto as potências ímpares
diferem pelo sinal. Isto nos permite economizar multiplicações
quando calculamos ![]() e
e
![]() simultaneamente.
Se n é par, podemos escrever
simultaneamente.
Se n é par, podemos escrever
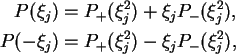
onde
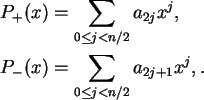
Ou seja, reduzimos o problema de calcular um polinômio de grau nem dois pontos ao problemas de calcular dois polinômios de grau n/2em um mesmo ponto, seguido de uma multiplicação, uma soma e uma subtração.
Se os ![]() sempre ocorrerem aos pares,
com por exemplo
sempre ocorrerem aos pares,
com por exemplo
![]() ,
o cálculo de
,
o cálculo de
![]() reduz-se ao cálculo
de
reduz-se ao cálculo
de
![]() seguido de 3n/2 operações.
seguido de 3n/2 operações.
O ideal é que pudéssemos repetir o processo acima, ou seja,
que n seja múltiplo de 4 e que também no conjunto
![]() os números ocorressem em pares diferindo apenas por sinal.
Reordenando os termos, podemos reformular esta condição como
os números ocorressem em pares diferindo apenas por sinal.
Reordenando os termos, podemos reformular esta condição como
![]() ,
ou, sem perda de generalidade,
como
,
ou, sem perda de generalidade,
como
![]() .
Para podermos repetir este processo um número máximo de vezes,
devemos tomar n como uma potência de 2 e
.
Para podermos repetir este processo um número máximo de vezes,
devemos tomar n como uma potência de 2 e
![]() ,
onde
,
onde
![]() .
Devemos assim tomar
.
Devemos assim tomar
![]() e a escolha
e a escolha ![]() parece particularmente simples.
parece particularmente simples.
Façamos agora uma estimativa de T(n), o número de operações usadas
neste algoritmo para calcular
![]() .
Já vimos que
T(n) = 2 T(n/2) + 3n/2; claramente T(1) = 0.
Daí temos T(2) = 3, T(4) = 12 e, por uma indução simples,
.
Já vimos que
T(n) = 2 T(n/2) + 3n/2; claramente T(1) = 0.
Daí temos T(2) = 3, T(4) = 12 e, por uma indução simples,
![]() .
Assim, é possível calcular
.
Assim, é possível calcular
![]() muito rápidamente.
muito rápidamente.
Reformulemos este problema na linguagem de álgebra linear. Temos

Falta aprender a recuperar os coeficientes de um polinômio P a partir
de
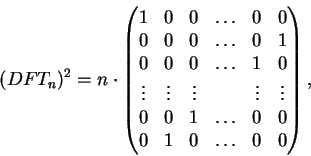
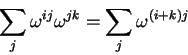
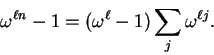
Reproduzimos abaixo o pseudo-código de [CB] para este algoritmo:
Input: O comprimento n (uma potência de 2);
uma raiz primitiva da unidade ![]() de ordem n;
um vetor
de ordem n;
um vetor
![]() de coeficientes complexos.
de coeficientes complexos.
Output: O vetor
![]() .
.
procedure
![]() ;
begin
if n = 1 then
A0 = a0;
else
;
begin
if n = 1 then
A0 = a0;
else
![]() ;
;
![]() ;
for k = 0 to n/2 - 1 do
;
for k = 0 to n/2 - 1 do
![]() ;
;
![]() ;
end
;
end
Até agora consideramos polinômios com coeficientes em
![]() mas o leitor atento já deve ter percebido que podemos usar
o mesmo algoritmo para multiplicar polinômios sobre qualquer corpo Kdesde que exista em K um elemento
mas o leitor atento já deve ter percebido que podemos usar
o mesmo algoritmo para multiplicar polinômios sobre qualquer corpo Kdesde que exista em K um elemento ![]() que seja
uma raiz da unidade de ordem n.
Um exemplo de corpo onde existe um tal
que seja
uma raiz da unidade de ordem n.
Um exemplo de corpo onde existe um tal ![]() é
é
![]() se
se
![]() .
Na verdade não é sequer necessário que os coeficientes estejam em um corpo:
podemos trabalhar sobre qualquer anel A onde exista
.
Na verdade não é sequer necessário que os coeficientes estejam em um corpo:
podemos trabalhar sobre qualquer anel A onde exista ![]() com as seguintes propriedades:
com as seguintes propriedades:
Lembramos que este algoritmo calcula corretamente o produto
dos polinômios P e Q desde que este produto tenha grau menor do que n.
Mais geralmente, estaremos encontrando o único polinômio de grau menor
que n que coincide com PQ em
![]() .
Como estamos tomando sempre
.
Como estamos tomando sempre
![]() temos
temos