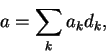
Quando escrevemos um inteiro a na base d,
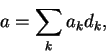
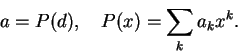
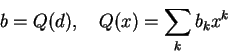
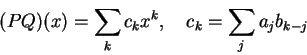
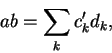
A dificuldade maior reside no fato que as contas descritas na seção anterior envolvem números complexos, e as partes real e imaginária destes números complexos são irracionais. Uma alternativa é fazer as contas usando variáveis do tipo double; teremos inevitavelmente erros de truncamento mas o fato de sabermos que a resposta final é um inteiro nos dá uma oportunidade de corrigir estes erros. É claro que precisamos ter o cuidado de evitar que os erros de truncamento somem mais do que 0,5: neste caso acabaríamos arredondando a resposta final para o inteiro errado. Esta possibilidade desastrosa pode ser evitada tomando d pequeno (e portanto grau grande, o que implica em uma transformada de Fourier de comprimento maior); também ajuda muito tomar o conjunto dos algarismos aceitáveis simétrico em relação ao zero, pois assim os produtos aj bk-jserão menores e terão sinais diferentes, o que evita que os coeficientes ck sejam grandes demais. Mesmo para inteiros bem maiores do que o maior primo conhecido existem valores de d que garantem o bom funcionamento deste método, um dos mais rápidos para multiplicar inteiros grandes (em parte porque a maioria dos computadores é capaz de multiplicar doubles com grande rapidez). Por isso, ele é usado pelo programa mprime-prime95, que encontrou os últimos 4 primos de Mersenne. Escrevemos um pequeno programa que usa o critério de Lucas-Lehmer para testar a primalidade de Mp e que multiplica usando FFT: as funções FFT estão em fft.c e o programa principal em fftest2.c.
Uma segunda alternativa é escolher um primo pe fazer a multiplicação de polinômios considerando os coeficientes
como elementos de
![]() .
Para recuperarmos os verdadeiros coeficientes do produto
(que são inteiros), precisamos ter o cuidado de garantir que
|ck| < p/2 onde
.
Para recuperarmos os verdadeiros coeficientes do produto
(que são inteiros), precisamos ter o cuidado de garantir que
|ck| < p/2 onde
![]() .
Um primo usado em alguns programas
4.2
é
p = 264 - 232 + 1,
que tem aliás várias propriedades especiais que o tornam
particularmente apropriado para nossa tarefa.
Com este valor de p, como
232 | p-1,
podemos fazer FFTs de comprimento 232 com
d = 216,
o que permite (em princípio) multiplicar inteiros de módulo menor do que
.
Um primo usado em alguns programas
4.2
é
p = 264 - 232 + 1,
que tem aliás várias propriedades especiais que o tornam
particularmente apropriado para nossa tarefa.
Com este valor de p, como
232 | p-1,
podemos fazer FFTs de comprimento 232 com
d = 216,
o que permite (em princípio) multiplicar inteiros de módulo menor do que
![]() ,
ou seja,
inteiros com alguns bilhões de algarismos;
o simples armazenamento de um tal inteiro exige memória maior
do que a que tem a maioria dos computadores atuais.
,
ou seja,
inteiros com alguns bilhões de algarismos;
o simples armazenamento de um tal inteiro exige memória maior
do que a que tem a maioria dos computadores atuais.
Mas estas alternativas, apesar de computacionalmente atraentes,
não satisfazem ao matemático puro pois funcionam para inteiros
menores do que um certo tamanho fixo (apesar de muito grande).
A segunda alternativa apresentada acima pode ser levada adiante tomando
primos cada vez maiores, mas não será fácil provar
que existem sempre primos com as propriedades desejadas.
Veremos agora como multiplicar inteiros de tamanho arbitrário
em tempo baixo fazendo as contas não em
![]() ,
mas em
,
mas em
![]() (mesmo 2K + 1 não sendo primo)
e assim evitaremos esta dificuldade.
Uma outra vantagem deste método é que será muito fácil multiplicar
por potências de
(mesmo 2K + 1 não sendo primo)
e assim evitaremos esta dificuldade.
Uma outra vantagem deste método é que será muito fácil multiplicar
por potências de ![]() (assim tornando rápidas as FFTs).
(assim tornando rápidas as FFTs).
Mais precisamente, mostraremos como multiplicar
inteiros (dados por suas expansões binárias) módulo 2N + 1;
esta é a versão simplificada de Schönhage de um algoritmo
devido a Schönhage e Strassen.
Se N for tomado suficientemente grande este algoritmo multiplica inteiros.
Consideraremos apenas valores de ![]() da forma
da forma
Para usar a multiplicação de polinômios, escrevemos os inteiros a e ba serem multiplicados na base d, i.e.,
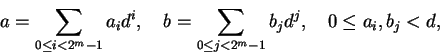
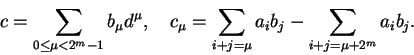
Sejam
![]() e
e
![]() .
Como
.
Como
![]() temos que
temos que ![]() é uma raiz da unidade em
é uma raiz da unidade em
![]() de ordem 2m:
este valor de
de ordem 2m:
este valor de ![]() pode ser usado para fazer FFT como na seção anterior;
temos
pode ser usado para fazer FFT como na seção anterior;
temos
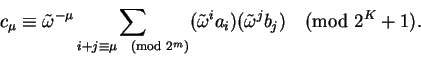
Falta apenas estimar o número de operações gasto por este algoritmo;
note que por operação aqui queremos dizer uma operação sobre bits.
Em todo o algoritmo,
efetuamos duas FFTs de comprimento 2m sobre
![]() ,
2m multiplicações ponto a ponto (também sobre
,
2m multiplicações ponto a ponto (também sobre
![]() )
e uma FFT inversa de comprimento 2m.
Observe que como
)
e uma FFT inversa de comprimento 2m.
Observe que como ![]() é uma potência de 2,
as multiplicações por potências de
é uma potência de 2,
as multiplicações por potências de ![]() que ocorrem nas FFTs
são rápidas pois são apenas translações dos algarismos;
mais precisamente, exigem no máximo CK operações cada uma
(para alguma constante positiva C).
Assim, cada FFT exige no máximo
que ocorrem nas FFTs
são rápidas pois são apenas translações dos algarismos;
mais precisamente, exigem no máximo CK operações cada uma
(para alguma constante positiva C).
Assim, cada FFT exige no máximo
![]() operações.
O número total T(N) de operações satisfaz assim a recorrência
operações.
O número total T(N) de operações satisfaz assim a recorrência