A função de Euler e o pequeno teorema de Fermat

Definimos $\varphi(n) = \vert({\mathbb{Z} }/(n))^\ast\vert$(onde |X| denota o número de elementos de X). A função $\varphi$ é conhecida como a função de Euler. Temos $\varphi(1) = \varphi(2) = 1$, e, para n > 2, $1 < \varphi(n) < n$. Se p é primo, $\varphi(p) = p-1$; mais geralmente $\varphi(p^k) = p^k - p^{k-1}$pois (a,p^k) = 1 se e somente se a não é múltiplo de pe há p^k-1 múltiplos de p no intervalo $0 \le a < p^k$.

Dizemos que os n números inteiros $a_1, a_2, \ldots, a_n$ formam um sistema completo de resíduos (ou s.c.r.) módulo n se $\{\overline{a_1}, \overline{a_2}, \ldots \overline{a_n} \} = {\mathbb{Z} }/(n)$, isto é, se os a_i representam todas as classes de congruência módulo n. Por exemplo, 0, 1, 2, ...n -1 formam um s.c.r. módulo n. Equivalentemente, podemos dizer que $a_1, a_2, \ldots, a_n$ formam um s.c.r. módulo nse e somente se $a_i \equiv a_j \pmod n$ implicar i = j. Os $\varphi(n)$ números inteiros $b_1, b_2, \ldots, b_{\varphi(n)}$formam um sistema completo de invertíveis (s.c.i.) módulo n se

$$\{\overline{b_1}, \overline{b_2}, \ldots \overline{b_{\varphi(n)}} \} = ({\mathbb{Z} }/(n))^\ast,$$

isto é, se os b_i representam todas as classes de congruências invertíveis módulo n. Também equivalentemente, $b_1, b_2, \ldots, b_{\varphi(n)}$ formam um s.c.i. módulo nse e somente se (b_i,n) = 1 para todo i e $a_i \equiv a_j \pmod n$ implicar i = j.

Proposição 1.12: Sejam $q, r, n \in {\mathbb{Z} }$, n > 0, q invertível módulo n, $a_1, a_2, \ldots, a_n$ um s.c.r. módulo n e $b_1, b_2, \ldots, b_{\varphi(n)}$ um s.c.i. módulo n. Então $qa_1 + r, qa_2 + r, \ldots, qa_n + r$formam um s.c.r. módulo n e $qb_1, qb_2,...qb_{\varphi(n)}$ formam um s.c.i. módulo n.

Dem: Se $qa_i + r \equiv qa_j + r \pmod n$ então n | q(a_i - a_j)e $a_i \equiv a_j \pmod n$, donde i = j; com isto provamos que $qa_1 + r, qa_2 + r, \ldots, qa_n + r$ formam um s.c.r..

Como (q,n) = (b_i,n) = 1, temos (q b_i, n) = 1. Por outro lado, se $qb_i \equiv qb_j \pmod n$temos $b_i \equiv b_j \pmod n$ (como no parágrafo anterior) e i = j. Isto conclui a demonstração.          $\blacksquare$

Teorema 1.13: (Euler) Sejam $a, n \in {\mathbb{Z} }$, n > 0, tais que (a, n) = 1. Então $a^{\varphi(n)} \equiv 1 \pmod n$.

Dem: Seja

$$b_1, b_2, \ldots.b_{\varphi(n)}$$

um s.c.i. módulo n. Pela proposição anterior,

$$ab_1, ab_2, \ldots ab_{\varphi(n)}$$

também formam um s.c.i. módulo n. Assim,

$$b_1 \cdot b_2 \cdots b_{\varphi(n)} \equiv ab_1 \cdot ab_2 \cdots ab_{\varphi(n)} \pmod n$$

pois módulo n os dois lados têm os mesmos fatores a menos de permutação. Mas isto pode ser reescrito como

$$a^{\varphi(n)} (b_1 \cdot b_2 \cdots b_{\varphi(n)}) \equiv 1 \cdot (b_1 \cdot b_2 \cdots b_{\varphi(n)}) \pmod n$$

e pelo corolário 1.9 isto implica $a^{\varphi(n)} \equiv 1 \pmod n$.          $\blacksquare$

Corolário 1.14: (Pequeno Teorema de Fermat) Se p é primo então, para todo inteiro a, $a^p \equiv a \pmod p$.

Dem: Se p|a, então $a^p \equiv a \equiv 0 \pmod p$. Caso contrário, $\varphi(p) = p-1$, $a^{p-1} \equiv 1 \pmod p$e novamente $a^p \equiv a \pmod p$.          $\blacksquare$

Outra demonstração do pequeno teorema de Fermat é por indução em ausando o binômio de Newton e algumas propriedades de números binomiais. Se 0 < i < p temos

$$\binom{p}{i} = \frac{p!}{i! (p-i)!} \equiv 0 \pmod p$$

pois há um fator p no numerador que não pode ser cancelado com nada que apareça no denominador. Os casos a = 0 e a = 1 do teorema são triviais. Supondo válido o teorema para a, temos
$$\begin{align}(a+1)^p &= a^p + \binom{p}{1} a^{p-1} + \cdots + \binom{p}{p-1} a + 1 \notag\\ &\equiv a^p + 1 \notag\\ &\equiv a + 1 \pmod p \notag \end{align}$$
e a indução está completa.

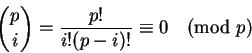
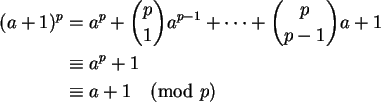
Corolário 1.15: Se (m, n) = 1 então $\varphi(mn) = \varphi(m) \varphi(n)$.

Dem: Construimos uma bijeção entre $({\mathbb{Z} }/(mn))^\ast$ e $({\mathbb{Z} }/(m))^\ast \times ({\mathbb{Z} }/(n))^\ast$, o que garante que estes conjuntos têm o mesmo número de elementos.          $\blacksquare$

Corolário 1.16: Se

$$n = p_1^{e_1} p_2^{e_2} \cdots p_m^{e_m}$$

com $p_1 < p_2 < \ldots < p_m$ e e_i > 0 para todo i então
$$\begin{align}\varphi(n) &= (p_1^{e_1} - p_1^{e_1 - 1})(p_2^{e_2} - p_2^{e_2 - 1}... ...frac{1}{p_2}}\right) \cdots \left({1 - \frac{1}{p_m}}\right). \notag \end{align}$$

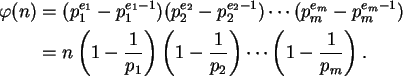
Dem: Isto segue da fórmula que já vimos para $\varphi(p^e)$ e do corolário anterior.          $\blacksquare$

Em particular, se n > 2 então $\varphi(n)$ é par.

Mais adiante estudaremos equações do segundo grau em ${\mathbb{Z} }/(p)$; vejamos desde já um pequeno resultado deste tipo que garante que os únicos a que são seus próprios inversos módulo p são 1 e -1.

Lema 1.17: Se p é primo então as únicas soluções de x² = 1em ${\mathbb{Z} }/(p)$ são 1 e -1. Em particular,se $x\in ({\mathbb{Z} }/(p))^\ast - \{1,-1\}$então $x^{-1} \neq x$ em ${\mathbb{Z} }/(p)$.

Dem: Podemos reescrever a equação como (x-1)(x+1) = 0, o que torna o resultado trivial.          $\blacksquare$

Teorema 1.18: (Wilson) Seja n > 4. Então $(n-1)! \equiv -1 \pmod n$ se n é primo e $(n-1)! \equiv 0 \pmod n$ se n é composto.

Dem: Se n é composto mas não é o quadrado de um primo podemos escrever n = ab com 1 < a < b < n: neste caso tanto a quanto b aparecem em (n-1)!e $(n-1)! \equiv 0 \pmod n$. Se n = p², p > 2, então p e 2p aparecem em (n-1)!e novamente $(n-1)! \equiv 0 \pmod n$; isto demonstra que para todo n composto, n > 4, temos $(n-1)! \equiv 0 \pmod n$.

Se n é primo podemos escrever $(n-1)! \equiv - (2 \cdot 3 \cdots n-2) \pmod n$; mas pelo lema anterior podemos juntar os inversos aos pares no produto do lado direito, donde $(n-1)! \equiv -1 \pmod n$.          $\blacksquare$