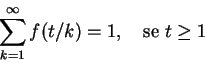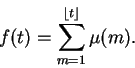A função de Möbius

Vejamos inicialmente uma propriedade da função $\varphi$.

Teorema 1.19: Para todo natural n,

$$\sum_{d\vert n}{\varphi(d)} = n.$$

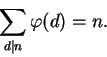
Este teorema segue facilmente da fórmula que provamos para $\varphi(n)$na seção anterior. Daremos entretanto uma demonstração bijetiva.

Dem: Considere as n frações

$$\frac{0}{n}, \frac{1}{n}, \ldots , \frac{n-1}{n}$$

e simplifique cada uma delas: obtemos assim, para cada d | n, $\varphi(d)$ frações com denominador d, donde segue a identidade do enunciado.

Mais formalmente, dado $\overline a \in {\mathbb{Z} }/(n)$, sejam d = n/(n,a) e a' = a/(n,a). Claramente $\overline{a'} \in ({\mathbb{Z} }/(d))^\ast$e definimos assim uma função de ${\mathbb{Z} }/(n)$ para a união disjunta dos conjuntos $({\mathbb{Z} }/(d))^\ast$, onde d varia sobre os divisores de n. A inversa desta função leva $\overline{a'} \in ({\mathbb{Z} }/(d))^\ast$em $\overline a$, a = na'/d, donde a função é uma bijeção.          $\blacksquare$

O processo de construir g a partir de f como

$$g(n) = \sum_{d\vert n} f(d)$$

é bastante comum em teoria dos números. Seria interessante poder inverter esta identidade para escrever f a partir de g. O teorema anterior nos mostra que se fazemos $f = \varphi$na equação acima temos g(n) = n; invertendo esta identidade teríamos uma fórmula para $\varphi$. O objetivo desta seção é mostrar como fazer este tipo de inversão.

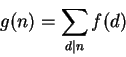
Definimos a função de Möbius $\mu: {\mathbb{N} }^\ast \to {\mathbb{Z} }$ por

$$\mu(n) = \begin{cases} (-1)^m,& \text{se $n = p_1 p_2 \cdots ... ...$ tem algum fator primo repetido em sua fatoração.} \end{cases}$$

Assim, $\mu(1) = \mu(6) = \mu(10) = 1$, $\mu(2) = \mu(3) = \mu(5) = \mu(7) = -1$ e $\mu(4) = \mu(8) = \mu(9) = 0$.

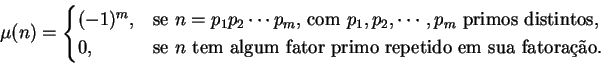
Lema 1.20: Para todo inteiro positivo n temos

$$\sum_{d\vert n} \mu(d) = \begin{cases} 1,& \text{se $n=1$,}\notag\\ 0,& \text{se $n>1$.}\notag\\ \end{cases}$$

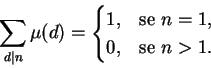
Dem: O caso n = 1 é trivial. Se n>1, seja p um divisor primo de n e seja n = p^e n' com $p \nmid n'$. Temos
$$\begin{align}\sum_{d\vert n} \mu(d) &= \sum_{d\vert n, p \nmid d} \mu(d) + \sum_... ...{d\vert n'} \mu(d) - \sum_{d'\vert n'} \mu(d') \notag\\ &= 0.\notag \end{align}$$
         $\blacksquare$

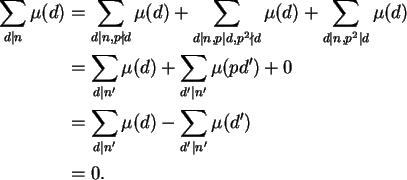
Teorema 1.21: (Fórmula de inversão de Möbius) Se para todo n > 0 temos

$$g(n) = \sum_{d\vert n} f(d)$$

então

$$f(n) = \sum_{d\vert n} \mu(n/d) g(d).$$

Observe que a fórmula do corolário 1.16 para $\varphi(n)$segue facilmente dos dois teoremas acima.

Dem: Basta provar que

$$f(n) = \sum_{d\vert n} \mu(n/d) \left({ \sum_{d'\vert d} f(d') }\right).$$

Mas, escrevendo d'' = n/d e m = n/d' temos

$$\sum_{d\vert n} \mu(n/d) \left({ \sum_{d'\vert d} f(d') }\rig... ... n} \left({ \sum_{d''\vert m} \mu(d'') }\right) f(n/m) = f(n).$$

         $\blacksquare$

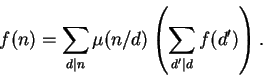
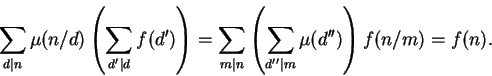
Teorema 1.22: (Segunda fórmula de inversão de Möbius) Sejam f e g funções reais com domínio $(0, +\infty)$ tais que f(t) = g(t) = 0 para todo t < 1. Se

$$g(x) = \sum_{k = 1}^{\infty} f\left({\frac{x}{k}}\right) = \sum_{1 = k}^{\lfloor x \rfloor} f\left({\frac{x}{k}}\right)$$

para todo x então então

$$f(x) = \sum_{k = 1}^{\infty} \mu(k) g\left({\frac{x}{k}}\righ... ...{1 = k}{\lfloor x \rfloor} \mu(k) g\left({\frac{x}{k}}\right).$$

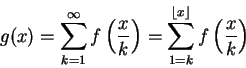
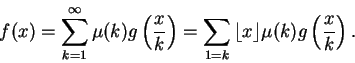
Dem: Basta provar que

$$f(x) = \sum_{k=1}^{\infty} \mu(k) \left({ \sum_{r = 1}^{\infty} f\left({\frac{x}{kr}}\right) }\right),$$

mas, tomando m = kr a última soma é igual a

$$\sum_{m=1}^{\infty} \left({ \left({ \sum_{k\vert m} \mu(k) }\right) f\left({\frac{x}{m}}\right) }\right)$$

que pelo lema é igual a f(x).          $\blacksquare$

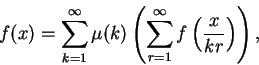
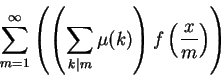
Apesar de não estar relacionada com o resto da nossa discussão, não podemos deixar de mencionar a seguinte conjectura.

Conjectura 1.23: (Hipótese de Riemann) Se $\alpha > 1/2$ então

$$\lim_{n \to \infty} \frac{1}{n^\alpha} \sum_{1 \le m}^n \mu(m) = 0.$$

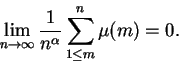
Esta é uma das formulações da famosa hipótese de Riemann, um dos problemas em aberto mais importantes da matemática.

Podemos reenunciar esta conjectura assim: seja $f: (0, +\infty) \to {\mathbb{R} }$ definida por f(t) = 0 se t<1 e

$$\sum_{k=1}^{\infty} f(t/k) = 1, \quad \text{se }t \ge 1$$

então, para todo $\alpha > 1/2$,

$$\lim_{t \to \infty} \frac{f(t)}{t^\alpha} = 0.$$

De fato, pela segunda fórmula de inversão de Möbius temos

$$f(t) = \sum_{m = 1}^{\lfloor t \rfloor} \mu(m).$$