As equações

O látice de Toda é um modelo matemático de propagação de ondas num cristal unidimensional ([T]). Sem mais delongas, considere a hamiltoniana H(x,y) para $(x,y) \in {\mathbb{R} }^{2n}$ dada por

$$H(x,y) = \frac{1}{2} \sum_{k=1}^n y_k^2 + \sum_{k=1}^{n-1} \exp(x_k - x_{k+1}) + P \exp(x_n - x_1),$$

onde x_k e y_k são respectivamente a posição e a velocidade da k-ésima partícula. A constante Ppode ser 0 ou 1: quando P é zero, estamos tratando do látice aberto, e quando P é 1, do látice periódico. A nomenclatura indica se as partículas 1 e n estão interagindo ou não. As n partículas estão em ${\mathbb{R} }$, têm todas a mesma massa e ocasionalmente ultrapassam-se umas às outras. De forma mais explícita, estamos considerando as equações
$$\begin{align}\dot{x_k} &= H_{y_k} = y_k, \quad k=1,\ldots, n,\notag\\ \dot{y_1... ...ot{y_n} &=-H_{x_n} = \exp(x_{n-1} - x_n) - P \exp(x_n - x_1), \notag \end{align}$$
onde $\dot{f}$ é a derivada no tempo da função f.

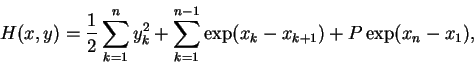
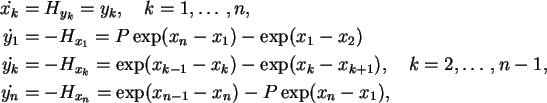
Os argumentos físicos habituais fornecem duas leis de conservação para o sistema: a própria hamiltoniana (energia) e o momento linear (que corresponde à velocidade do centro de massa do sistema). O primeiro fato milagroso associado à dinâmica desse sistema, descoberto por Flaschka ([F]), é que é possível descrever de forma simples n leis de conservação, tanto para o caso aberto quanto para o caso periódico -- isso se faz em dois passos. No caso aberto, comece mudando de variáveis,
$$\begin{align}a_k &= -y_k/2, \quad k=1,\ldots,n \notag\\ 2 b_k &= \exp[(x_k -x_{k+1})/2],\quad k = 1,\ldots,n-1, \notag \end{align}$$
para obter
$$\begin{align}\dot{a_1} &= 2b_1^2,\notag\\ \dot{a_k} &= 2(b_k^2 - b_{k-1}^2), \... ...tag\\ \dot{b_k} &= b_k(a_{k+1} - a_k), \quad k=1,\ldots,n-1.\notag \end{align}$$
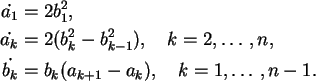
Perdemos um grau de liberdade no processo: 2n variáveis (x_k,y_k)viraram 2n-1 variáveis (a_k,b_k). O grau que falta é justamente a conservação do momento linear: os detalhes que mostram que nada se perdeu no estudo da dinâmica podem ser encontrados em [To]. Agora, considere as matrizes tridiagonais

$$L = \begin{pmatrix}a_1 & b_1 & 0 & \ldots \\ b_1 & a_2 & b_... ...ts&\ldots&-b_{n-1}\\ \ldots&\ldots&b_{n-1}& 0 \end{pmatrix}.$$

Uma conta mostra que as equações de evolução das variáveis a_k e b_k correspondem à evolução matricial

$$\dot{L} = [L,B] = LB - BL.$$

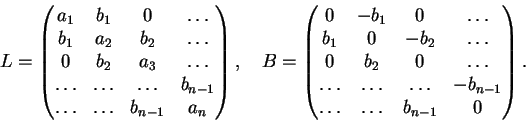
No caso periódico, alterações mínimas do argumento acima transformam a evolução de (x,y) na equação

$$\dot{M} = [M,C] = MC - CM,$$

onde M e C são matrizes tridiagonais periódicas,

$$M = \begin{pmatrix}a_1 & b_1 & 0 & \ldots & b_n \\ b_1 & a_... ...ts&\ldots&-b_{n-1}\\ -b_n&0&\ldots&b_{n-1}& 0 \end{pmatrix}.$$

Note que a diferença entre L e M, assim como entre B e C, está nas posições (1,n) e (n,1) das matrizes, que apropriadamente vinculam as partículas 1 e n.

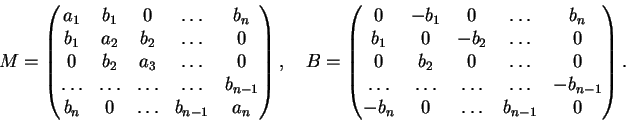
As evoluções matriciais têm uma forma especial: L e Mevoluem de acordo com pares de Lax ([L]), e disso segue imediatamente que os autovalores de L e M não mudam no tempo, como veremos mais adiante -- esse fato, descoberto poucos anos antes, orientou Flaschka na reformulação das evoluções em (x,y). Aliás, a conservação de momento e de energia correspondem à conservação do traço e da soma dos quadrados dos autovalores de L (ou M) (mais detalhes em [To]).