Se
![]() denota o grupo das unidades
de um anel A então
o determinante é um morfismo de grupos
denota o grupo das unidades
de um anel A então
o determinante é um morfismo de grupos
| (I.1.1) |
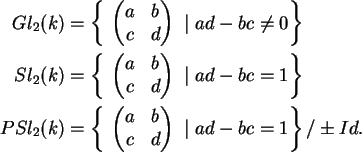
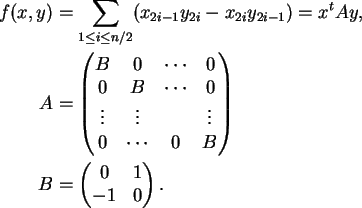
No caso de
![]() ser não-singular,
bilinear e simétrica, e o
corpo k ter característica diferente de 2,
os grupos de matrizes que preservam
ser não-singular,
bilinear e simétrica, e o
corpo k ter característica diferente de 2,
os grupos de matrizes que preservam
![]() são os chamados
grupos ortogonais; em geral a classe
de isomorfismo destes
grupos depende da escolha de
são os chamados
grupos ortogonais; em geral a classe
de isomorfismo destes
grupos depende da escolha de
![]() ,
e
logo estes grupos devem vir denotados por
On(k,f). O número de formas
,
e
logo estes grupos devem vir denotados por
On(k,f). O número de formas
![]() que geram grupos não isomorfos depende do corpo
de constantes k. O determinante de qualquer
matriz em On(k,f) é
que geram grupos não isomorfos depende do corpo
de constantes k. O determinante de qualquer
matriz em On(k,f) é ![]() ,
e o grupo
de matrizes de determinante um
em
,
e o grupo
de matrizes de determinante um
em
![]() é denotado por SOn(k,f).
O centro
Z(On(k,f)) consiste
nas matrizes
é denotado por SOn(k,f).
O centro
Z(On(k,f)) consiste
nas matrizes
![]() onde
onde
![]() ,
e o quociente
,
e o quociente
![]() é denotado
PSOn(k,f).
O núcleo SOn(k,f) de
é denotado
PSOn(k,f).
O núcleo SOn(k,f) de
No caso de k ser dotado de uma involução
![]() e
e
![]() ser hermitiana os grupos
de matrizes não-singulares que preservam esta
forma são os grupos unitários; como no caso
dos grupos ortogonais, os grupos unitários
dependem da escolha de
ser hermitiana os grupos
de matrizes não-singulares que preservam esta
forma são os grupos unitários; como no caso
dos grupos ortogonais, os grupos unitários
dependem da escolha de
![]() ,
e devem ser denotados por Un(k,f). As matrizes
em Un(k,f) de determinante um formam um
subgrupo SUn(k,f). O centro
Z(Un(k,f)
de Un(k,f) é formado
por
,
e devem ser denotados por Un(k,f). As matrizes
em Un(k,f) de determinante um formam um
subgrupo SUn(k,f). O centro
Z(Un(k,f)
de Un(k,f) é formado
por
![]() ,
e
,
e
Exemplos e Exercícios
1. Grupos clássicos sobre um corpo
finito. O corpo finito com q=pr
elementos será denotado por ![]() .
Temos
.
Temos
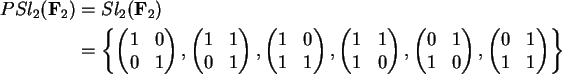
donde
![]() é isomorfo ao
grupo S3 e o subgrupo
é isomorfo ao
grupo S3 e o subgrupo
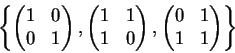
Sobre ![]() o grupo
PSl2 consiste de classes de matrizes;
a descrição abaixo identifica
cada matriz com a classe a que pertence:
o grupo
PSl2 consiste de classes de matrizes;
a descrição abaixo identifica
cada matriz com a classe a que pertence:
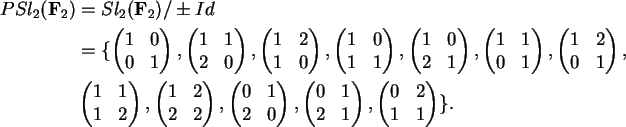
donde
![]() é isomorfo ao
grupo A4 e
o subgrupo
é isomorfo ao
grupo A4 e
o subgrupo
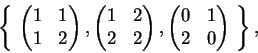
Estes são, no entanto,
os únicos casos em que
![]() não é simples.
Para n=2 e
não é simples.
Para n=2 e ![]() ,
e para n> 2
os grupos
,
e para n> 2
os grupos
![]() são
simples e formam a família
mais tratável (a parte os grupos
cíclicos de ordem prima e os
grupos alternados An para
são
simples e formam a família
mais tratável (a parte os grupos
cíclicos de ordem prima e os
grupos alternados An para ![]() )
no grande teorema de classificação
de grupos finitos simples (ver o material
recolhido em 3. abaixo). A ordem de
)
no grande teorema de classificação
de grupos finitos simples (ver o material
recolhido em 3. abaixo). A ordem de
![]() é dada por
é dada por
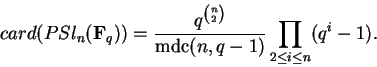
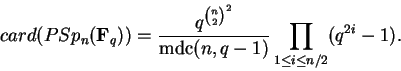
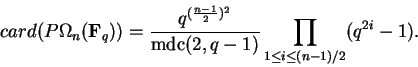
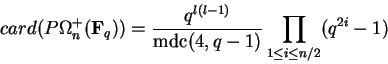
.
\end{displaymath}](img744.gif)
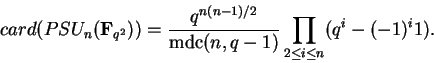
2. A simplicidade de
![]() .
No caso de A=k ser um corpo o determinante
(I.1.1) como homomorfismo de
grupos admite uma seção
.
No caso de A=k ser um corpo o determinante
(I.1.1) como homomorfismo de
grupos admite uma seção
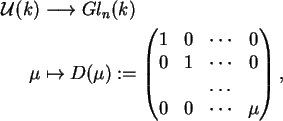
e realiza Gln(k) como produto semi-direto
de Sln(k) e
![]() .
Isto significa que toda matriz
.
Isto significa que toda matriz
![]() se escreve de forma única
se escreve de forma única
| (2.1) |
| (2.2) |
Se n=2 e
![]() então
o grupo
então
o grupo
![]() se manifesta
como o grupo de transformações
lineares fracionárias
se manifesta
como o grupo de transformações
lineares fracionárias
| (2.3) |
 a normalidade de H implica
a normalidade de H implica
Por causa de (2.2) o conjunto
Para provar a simplicidade de
![]() é suficiente provar que se H for
um subgrupo normal de
é suficiente provar que se H for
um subgrupo normal de
![]() contendo o centro
contendo o centro
![]() então necessariamnete
então necessariamnete
![]() .
Se
H contiver a matriz
.
Se
H contiver a matriz
 ,
para
,
para
![]() então H também
contem, para
então H também
contem, para
 ,
a matriz
,
a matriz
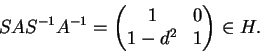
Assim, resta mostrar que H
contem alguma matriz
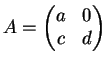 com
com
![]() .
Seja
.
Seja
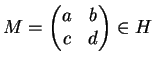 matriz em H
não no centro
matriz em H
não no centro
![]() com polinômio
mínimo
com polinômio
mínimo
![]() .
Se este polinômio
se fatorar em
.
Se este polinômio
se fatorar em ![]() então M é similar
a uma matriz diagonal, caso contrário M é
similar à matriz na forma canônica racional
então M é similar
a uma matriz diagonal, caso contrário M é
similar à matriz na forma canônica racional
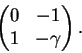
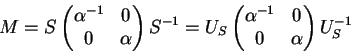
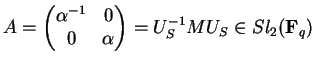 satisfaz
as exigências, já que
satisfaz
as exigências, já que
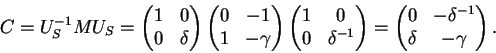
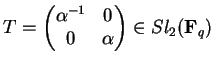 vale que H certamente conterá
vale que H certamente conterá
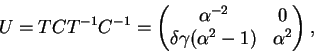
Valem os isomorfismos
3. Um olhar de relance sobre grupos simples.
Para listar todos os grupos simples finitos
nos é possível, ao final do século XX,
enfim seguir o fenomenal conselho do rei de copas
em Alice no País das Maravilhas: ``Comece
pelo começo e vá
prosseguindo até chegar ao fim, e
então pare''. Esta lista, agora afinal completa
(ao que parece, pace opiniões divergentes
sobre a insuficiência da documentação
de certas provas), começa de uma forma
modesta: os grupos cíclicos
![]() de ordem finita p são simples,
não tendo nenhum subgrupo normal,
de fato não tendo
subgrupo algum. Em ordem de complexidade
vem os grupos alternados
An para
de ordem finita p são simples,
não tendo nenhum subgrupo normal,
de fato não tendo
subgrupo algum. Em ordem de complexidade
vem os grupos alternados
An para ![]() ,
mas não só a prova
da simplicidade destes grupos é
mais complicada como existem as ``exceções''
A3 e A4.
,
mas não só a prova
da simplicidade destes grupos é
mais complicada como existem as ``exceções''
A3 e A4.
Os próximos grupos simples da lista são os grupos clássicos sobre corpos finitos listados em 1., que tem uma forte tendência à simplicidade, embora existam exceções. O padrão da procura é as provas de simplicidade ficarem cada vez mais complexas em cada família infinita, com esta complexidade atestada pela existência de exceções, até o ponto em que aparecem exceções fora das famílias: os grupos simples esporádicos, vinte e seis grupos simples que não se enquadram em nenhuma das famílias infinitas.
Os grupos alternados e os grupos clássicos
se manifestam a partir de uma ação natural,
os grupos alternados An aparecendo como
permutações pares do conjunto
![]() e os grupos clássicos como homorfismos de
espaços vetoriais ou de espaços projetivos
(submetidos a restrições de preservar formas).
Outros grupos simples finitos foram descobertos
em situações similares, como grupos de
permutação de sistemas combinatórios.
A situação geral pode ser formalizada da
seguinte forma: dada uma categoria C e
um objeto C de C,
uma representação de um grupo G
em C é um homomorfismo de grupos
e os grupos clássicos como homorfismos de
espaços vetoriais ou de espaços projetivos
(submetidos a restrições de preservar formas).
Outros grupos simples finitos foram descobertos
em situações similares, como grupos de
permutação de sistemas combinatórios.
A situação geral pode ser formalizada da
seguinte forma: dada uma categoria C e
um objeto C de C,
uma representação de um grupo G
em C é um homomorfismo de grupos
Tipicamente C é uma categoria concreta,
admitindo um funtor de esquecimento
![]() :
os objetos de C
são conjuntos dotados de estrutura. Se
:
os objetos de C
são conjuntos dotados de estrutura. Se ![]() for uma representação em C, para
for uma representação em C, para ![]() o grupo de isotropia Gc é o subgrupo
de G dado por
o grupo de isotropia Gc é o subgrupo
de G dado por
Dada uma representação ![]() de G em C
define-se, para n inteiro positivo,
de G em C
define-se, para n inteiro positivo,
O grupo clássico
![]() age
naturalmente na reta projetiva
age
naturalmente na reta projetiva
![]() ,
o grupo de isotropia de
,
o grupo de isotropia de ![]() sendo dado por
sendo dado por
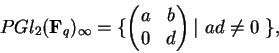
Se q=(q')2 for um quadrado então
![]() é
automorfismo involutivo de
é
automorfismo involutivo de ![]() ,
que pode ser
extendido a um automorfismo da reta projetiva
,
que pode ser
extendido a um automorfismo da reta projetiva
![]() por
por
![]() .
Vendo
.
Vendo
![]() como grupo de
transformações lineares fracionárias
((2.3), isto é, identificando
como grupo de
transformações lineares fracionárias
((2.3), isto é, identificando
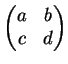 com
com
![]() ),
e considerando o grupo
),
e considerando o grupo
![]() de transformações
na reta projetiva
de transformações
na reta projetiva
![]() dado por
dado por
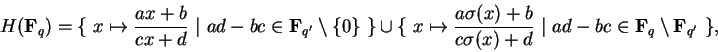
Existem grupos estritamente 4-transitivos
e grupos 5-transitivos (não isomorfos
a grupos simétricos e alternados), mas segue do
teorema de classificação que não existem
grupos n-transitivos para ![]() .
De fato,
Jordan mostrou em 1872
que para
.
De fato,
Jordan mostrou em 1872
que para ![]() só podem existir
grupos estritamente n-transitivos (não isomorfos
a grupos simétricos ou alternados) se n=4, e neste
caso o grau da representação é 11, ou n=5,
e neste caso o grau da representação é 12.
Estas cotas são atingidas: existem grupos assim.
De fato, existem grupos assim que são grupos simples
e esporádicos (isto é,
não isomorfos a nenhum elemento das famílias
clássicas).
Estes grupos são os grupos M11 e M12
descobertos por Mathieu em 1861.
só podem existir
grupos estritamente n-transitivos (não isomorfos
a grupos simétricos ou alternados) se n=4, e neste
caso o grau da representação é 11, ou n=5,
e neste caso o grau da representação é 12.
Estas cotas são atingidas: existem grupos assim.
De fato, existem grupos assim que são grupos simples
e esporádicos (isto é,
não isomorfos a nenhum elemento das famílias
clássicas).
Estes grupos são os grupos M11 e M12
descobertos por Mathieu em 1861.
Frequentemente a categoria C em que se
representa um grupo
tem aspectos combinatórios interessantes.
Por exemplo, um sistema de Steiner
![]() de tipo
(r,s,t) consiste em um conjunto A de cardinalidade
t e um conjunto
de tipo
(r,s,t) consiste em um conjunto A de cardinalidade
t e um conjunto ![]() de subconjuntos
de subconjuntos
![]() ,
com
card(Bi)=s tal que
para cada subconjunto
,
com
card(Bi)=s tal que
para cada subconjunto
![]() com card(C)=r existe exatamente um i
com
com card(C)=r existe exatamente um i
com
![]() .
Uma estrutura assim
admite morfismos evidentes
(os subconjuntos Bi de um sistema sendo levados
nos subconjuntos do outro),
definindo uma categoria St que, por serem
como são as coisas, é muito pequena:
neste mundo existem poucos sistemas de
Steiner. Por exemplo, a menos de isomorfismo
só existe um sistema
de Steiner
.
Uma estrutura assim
admite morfismos evidentes
(os subconjuntos Bi de um sistema sendo levados
nos subconjuntos do outro),
definindo uma categoria St que, por serem
como são as coisas, é muito pequena:
neste mundo existem poucos sistemas de
Steiner. Por exemplo, a menos de isomorfismo
só existe um sistema
de Steiner
![]() de tipo
(r,s,t)=(5,6,12), ou de tipo (5,8,24).
No entanto, uma surpresa:
de tipo
(r,s,t)=(5,6,12), ou de tipo (5,8,24).
No entanto, uma surpresa:
Dado um sistema de Steiner de tipo (r,s,t)
sobre um conjunto A, destacando um elemento ![]() define-se um sistema de Steiner de tipo
(r-1,
s-1,t-1) sobre
define-se um sistema de Steiner de tipo
(r-1,
s-1,t-1) sobre
![]() tomando como
subconjuntos
tomando como
subconjuntos
![]() onde Bi
são todos os subconjuntos do sistema
original que contem a.
Dado o sistema
onde Bi
são todos os subconjuntos do sistema
original que contem a.
Dado o sistema
![]() ,
o sistema
,
o sistema
![]() que resulta deste processo
tem como grupo de automorfismos o grupo de
Mathieu M11, e dado
o sistema
que resulta deste processo
tem como grupo de automorfismos o grupo de
Mathieu M11, e dado
o sistema
![]() ,
o sistema
,
o sistema
![]() que resulta deste processo
tem como grupo de automorfismos um quarto grupo simples
M23 ainda descoberto por Mathieu. O grupo
M11 é o grupo de isotropia de um símbolo
de M12, e o grupo
M23 é o grupo de isotropia de um símbolo
de M24. O grupo de isotropia de um símbolo
de M23 é ainda um último grupo simples
M22 descoberto por Mathieu; este grupo M22
é um subgrupo de
que resulta deste processo
tem como grupo de automorfismos um quarto grupo simples
M23 ainda descoberto por Mathieu. O grupo
M11 é o grupo de isotropia de um símbolo
de M12, e o grupo
M23 é o grupo de isotropia de um símbolo
de M24. O grupo de isotropia de um símbolo
de M23 é ainda um último grupo simples
M22 descoberto por Mathieu; este grupo M22
é um subgrupo de
![]() de índice dois, onde
de índice dois, onde
![]() é o sistema de Steiner
obtido a partir de
é o sistema de Steiner
obtido a partir de
![]() .
.
Outros grupos começam a se repetir, ou não são
simples: por exemplo, o grupo de isotropia de
um símbolo de M23 é o grupo clássico
![]() (e logo não é um grupo
novo, esporádico), enquanto que o grupo de
isotropia de um símbolo de M11 tem um
subgrupo (isomorfo a
(e logo não é um grupo
novo, esporádico), enquanto que o grupo de
isotropia de um símbolo de M11 tem um
subgrupo (isomorfo a
![]() )
de índice dois (e logo normal)
e assim este grupo não é simples.
)
de índice dois (e logo normal)
e assim este grupo não é simples.
Os grupos de Mathieu
M11,M12,M22,M23
e M24 foram os únicos grupos esporádicos
descobertos no século XIX. Suas ordens são dadas
por:
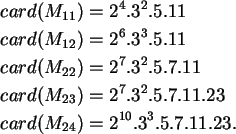
Os demais vinte e cinco grupos esporádicos
foram descobertos no século XX; de fato, foram
decobertos entre 1950 e 1980.
Referências.
A bibliografia sobre grupos clássicos é
imensa. Os livros de Weyl [W] e de
Dieudonné [D] são clássicos.
A classificação dos grupos simples deveria ser cantada em versos épicos. Enquanto tal não acontece, permanece dispersa em uma quantidade de artigos feitos por e para especialistas. Quem mais trabalhou para remediar este estado de coisas foi Daniel Gorenstein, do qual citamos [Go].