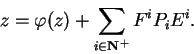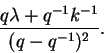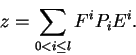Next: Apêndice A: A Linguagem
Up: Grupos Quânticos
Previous: A Álgebra Envolvente
Nesta seção
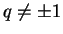 ,
de modo que
1/(q-q-1) está bem definido. Isto será
aproveitado na definição
,
de modo que
1/(q-q-1) está bem definido. Isto será
aproveitado na definição
Estes elementos aparecem substituindo inteiros
em fórmulas nos módulos de
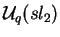 .
Os ``fatoriais'' e ``coeficientes
binomiais'' que surgem são
definidos por
.
Os ``fatoriais'' e ``coeficientes
binomiais'' que surgem são
definidos por
Valem
Se q não for raiz da unidade então
![$[n]_q\not= 0$](img1233.gif) .
.
O objetivo agora é quantizar o que foi feito
em 1. de I.5 para representações
de sl2. Os módulos simples de dimensão finita
de
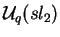 são também ``módulos
de peso máximo'', mas agora os vetores
de peso máximo são autovetores de K.
Especificamente, se V for um módulo
sobre
são também ``módulos
de peso máximo'', mas agora os vetores
de peso máximo são autovetores de K.
Especificamente, se V for um módulo
sobre
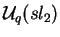 então se
então se
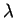 é chamado de peso, e para
é chamado de peso, e para
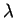 um peso o autoespaço de K associado
a
um peso o autoespaço de K associado
a 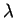 é denotado
é denotado 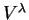 .
Valem
.
Valem
Se
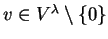 for tal que
Ev=0 então v é dito vetor de
peso máximo. Um módulo de peso
máximo é um módulo gerado por um
vetor de peso máximo.
for tal que
Ev=0 então v é dito vetor de
peso máximo. Um módulo de peso
máximo é um módulo gerado por um
vetor de peso máximo.
Sob a hipótese 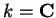 todo módulo de
dimensão finita tem um vetor de peso máximo.
A demosntração segue os passos da apresentada
para o caso clássico.
todo módulo de
dimensão finita tem um vetor de peso máximo.
A demosntração segue os passos da apresentada
para o caso clássico.
Valem as seguintes relações análogas
às clássicas encontradas em 1.
de (I.4), para um vetor de peso máximo V
de peso 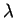 :
:
e
Assim,
![$\{ \frac{F^iv}{[i]_q!}\}$](img1241.gif) é uma sequência
de autovetores de K com autovalores distintos
e, novamente, deve existir um maior inteiro i
para o qual
é uma sequência
de autovetores de K com autovalores distintos
e, novamente, deve existir um maior inteiro i
para o qual
![$\frac{F^iv}{[i]_q!}$](img1242.gif) não seja nulo.
De fato,
pelas relações acima
não seja nulo.
De fato,
pelas relações acima
e logo
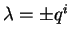 .
Como no caso clássico
segue que se o módulo for simples então é
módulo de peso máximo de dimensão i+1, e
estes módulos são denotados por
.
Como no caso clássico
segue que se o módulo for simples então é
módulo de peso máximo de dimensão i+1, e
estes módulos são denotados por
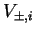 ,
onde o sinal é dado por
,
onde o sinal é dado por
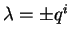 .
Também
.
Também
![$\{ \frac{F^jv}{[j]_q!}\}_{i=0,\ldots ,i}$](img1246.gif) é base de
é base de
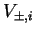 ,
e a ação de K
é diagonal com i+1 autovalores distintos
,
e a ação de K
é diagonal com i+1 autovalores distintos
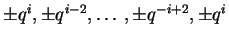 (com sinais combinando: ou todos +
ou todos -). Quaisquer dois vetores de peso
máximo diferem por uma constante multiplicativa.
Finalmente, qualquer módulo simples de
dimensão finita sobre
(com sinais combinando: ou todos +
ou todos -). Quaisquer dois vetores de peso
máximo diferem por uma constante multiplicativa.
Finalmente, qualquer módulo simples de
dimensão finita sobre
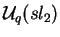 é um módulo de peso máximo, e dois
destes não são isomorfos. Assim, para cada
dimensão i existem exatamente dois
módulos simples sobre
é um módulo de peso máximo, e dois
destes não são isomorfos. Assim, para cada
dimensão i existem exatamente dois
módulos simples sobre
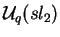 não isomorfos V+,i-1 e V-,i-1.
não isomorfos V+,i-1 e V-,i-1.
Para um escalar 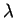 qualquer (não
da forma
qualquer (não
da forma
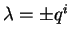 ), as seguintes
relações impostas sobre o espaço
vetorial
), as seguintes
relações impostas sobre o espaço
vetorial
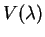 de dimensão infinita
com base enumerável
de dimensão infinita
com base enumerável
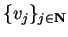
e
Fvj-1=[i]qvj
dotam
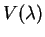 da estrutura de um módulo
sobre
da estrutura de um módulo
sobre
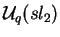 ,
onde v0 é vetor
de peso máximo. Estes módulos são ditos
módulos de Verma e são universais
no sentido de que todo módulo de peso
màximo V sobre
,
onde v0 é vetor
de peso máximo. Estes módulos são ditos
módulos de Verma e são universais
no sentido de que todo módulo de peso
màximo V sobre
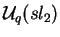 com peso máximo
com peso máximo 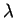 é quociente
de
é quociente
de
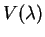 .
.
O comutador de K em
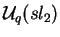 ,
denotado por
,
denotado por
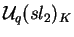 é o conjunto de elementos de
é o conjunto de elementos de
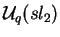 que comutam com K. Como a conjugação
por K atua na base de
que comutam com K. Como a conjugação
por K atua na base de
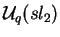 por
por
K(FiKlEj)K-1=q2(j-i)FiKlEj,
vale que
onde
![$P_i\in k[T,T^{-1}]$](img1254.gif) .
o ideal à esquerda cal I
de
.
o ideal à esquerda cal I
de
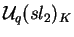 gerado por E,
gerado por E,
é dado também por
e vale
Isto se vê diretamente.
Assim
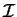 é um ideal bilateral de
é um ideal bilateral de
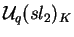 e a projeção
e a projeção
é um morfismo em
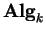 dito o
homomorfismo de Harish-Chandra.
dito o
homomorfismo de Harish-Chandra.
Se V for módulo de peso máximo de
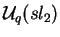 com peso máximo
com peso máximo
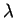 então para todo elemento central
então para todo elemento central
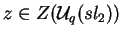 e todo
e todo  vale
vale
De fato, z pode ser escrito
Se v0 for o vetor de peso máximo
então Ev0=0, e como
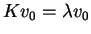 vale
vale
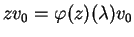 .
Mas
.
Mas
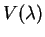 é gerado por v0, e logo
para todo
é gerado por v0, e logo
para todo
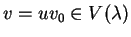 com
com
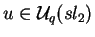 vale
vale
Em particular, o elemento de Casimir
quântico age por multiplicação pelo
escalar
A restrição de homomorfismo de
Harish-Chandra 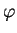 ao centro
ao centro
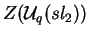 é injetiva,
já que se
é injetiva,
já que se
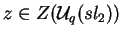 é não nulo e satisfaz
é não nulo e satisfaz
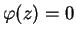 é possível escrever
é possível escrever
Tomando um módulo de Verma
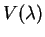 com
com
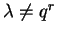 para nenhum r,
então Evi=0 só para i=0, e aplicando
z em vi vale que
para nenhum r,
então Evi=0 só para i=0, e aplicando
z em vi vale que
por um lado, e por outro,
para 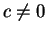 .
Segue que
.
Segue que
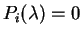 e haveria um polinômio
com infinitas raízes, um absurdo.
e haveria um polinômio
com infinitas raízes, um absurdo.




Next: Apêndice A: A Linguagem
Up: Grupos Quânticos
Previous: A Álgebra Envolvente
Nicolau C. Saldanha
1999-08-10
![\begin{displaymath}[n]_q=\frac{q^n-q^{-n}}{q-q^{-1}}=q^{n-1}+
q^{n-3}+\cdots +q^{-n+3}+q^{-n+1}.\end{displaymath}](img1230.gif)
![\begin{displaymath}[n]_q=\frac{q^n-q^{-n}}{q-q^{-1}}=q^{n-1}+
q^{n-3}+\cdots +q^{-n+3}+q^{-n+1}.\end{displaymath}](img1230.gif)
![\begin{displaymath}[n]_q!=[1]_q.[2]_q.\cdots ,[n]_q,
\qquad \binom{n}{k}_q=\frac{[n]_q!}{[k]_q!
[n-k]_q!}.\end{displaymath}](img1231.gif)
![]() são também ``módulos
de peso máximo'', mas agora os vetores
de peso máximo são autovetores de K.
Especificamente, se V for um módulo
sobre
são também ``módulos
de peso máximo'', mas agora os vetores
de peso máximo são autovetores de K.
Especificamente, se V for um módulo
sobre
![]() então se
então se
![]() todo módulo de
dimensão finita tem um vetor de peso máximo.
A demosntração segue os passos da apresentada
para o caso clássico.
todo módulo de
dimensão finita tem um vetor de peso máximo.
A demosntração segue os passos da apresentada
para o caso clássico.
![]() :
:
![\begin{displaymath}K\frac{F^iv}{[i]_q!}=\lambda q^{-2i}
\frac{F^iv}{[i]_q!},\end{displaymath}](img1238.gif)
![\begin{displaymath}E\frac{F^iv}{[i]_q!}=\frac{q^{-(i-1)}\lambda -q^{i-1}
\lambda^{-1}}{q-q^{-1}}
\frac{F^{i-1}v}{[i-1]_q!},\end{displaymath}](img1239.gif)
![\begin{displaymath}F\frac{F^{i-1}v}{[i-1]_q!}=[i]_q
\frac{F^iv}{[i]_q!}.\end{displaymath}](img1240.gif)
![\begin{displaymath}0=E
\frac{F^{i+1}v}{{i+1}!}=
\frac{q^{-i}\lambda -q^i
\lambda^{-1}}{q-q^{-1}}
\frac{F^iv}{[i]_q!},\end{displaymath}](img1243.gif)
![]() qualquer (não
da forma
qualquer (não
da forma
![]() ), as seguintes
relações impostas sobre o espaço
vetorial
), as seguintes
relações impostas sobre o espaço
vetorial
![]() de dimensão infinita
com base enumerável
de dimensão infinita
com base enumerável
![]()
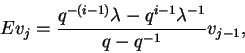
![]() ,
denotado por
,
denotado por
![]() é o conjunto de elementos de
é o conjunto de elementos de
![]() que comutam com K. Como a conjugação
por K atua na base de
que comutam com K. Como a conjugação
por K atua na base de
![]() por
por
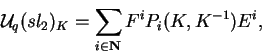
![]() é um ideal bilateral de
é um ideal bilateral de
![]() e a projeção
e a projeção
![]() com peso máximo
com peso máximo
![]() então para todo elemento central
então para todo elemento central
![]() e todo
e todo ![]() vale
vale